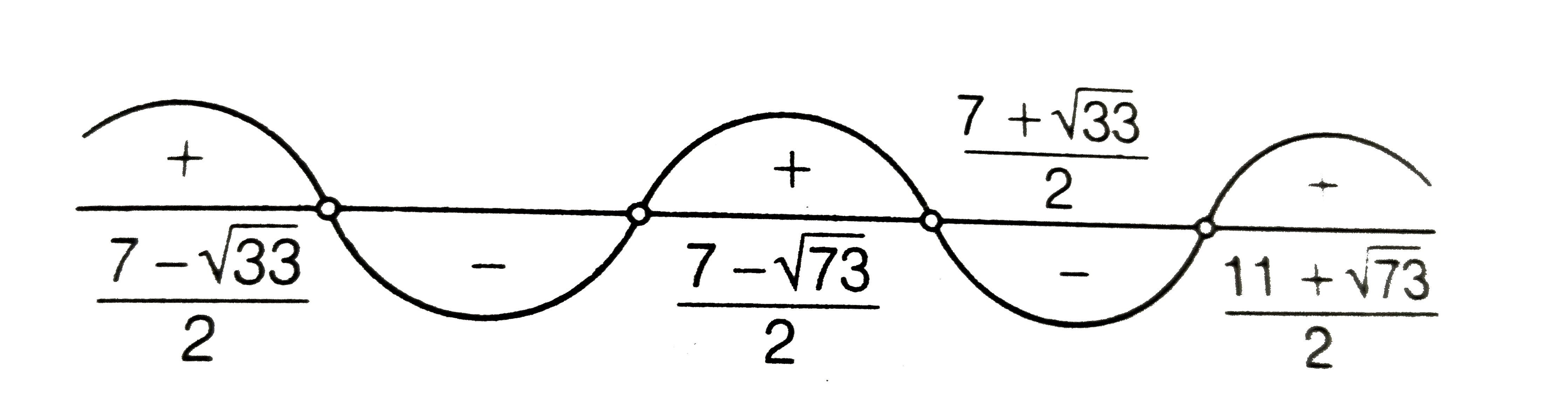Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
THEORY OF EQUATIONS
ARIHANT MATHS|Exercise Exercise (Questions Asked In Previous 13 Years Exam)|35 VideosTHEORY OF EQUATIONS
ARIHANT MATHS|Exercise Exercise (Statement I And Ii Type Questions)|7 VideosTHE STRAIGHT LINES
ARIHANT MATHS|Exercise The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)|1 VideosTHREE DIMENSIONAL COORDINATE SYSTEM
ARIHANT MATHS|Exercise Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam|2 Videos
Similar Questions
Explore conceptually related problems
ARIHANT MATHS-THEORY OF EQUATIONS-Exercise (Subjective Type Questions)
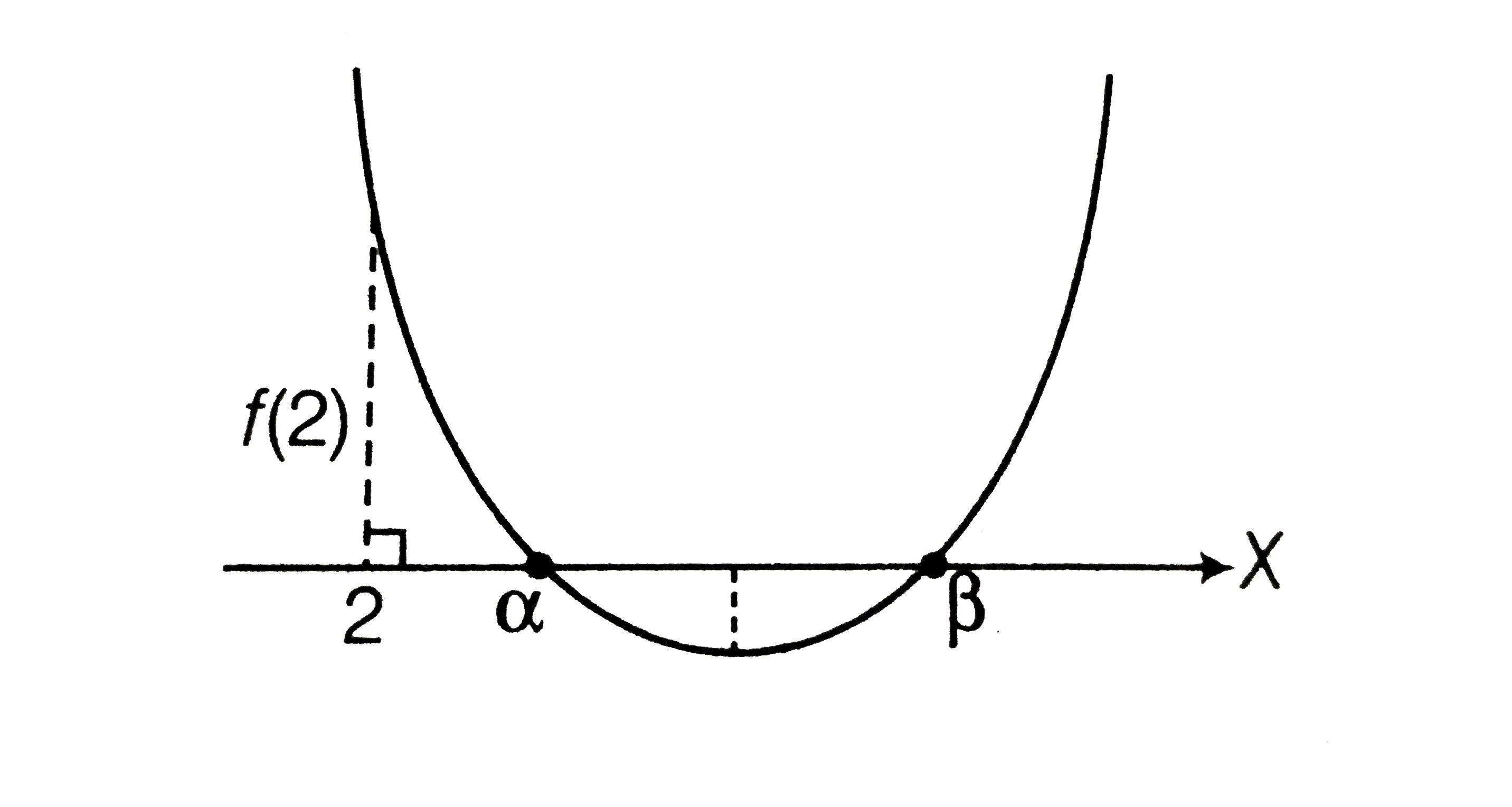
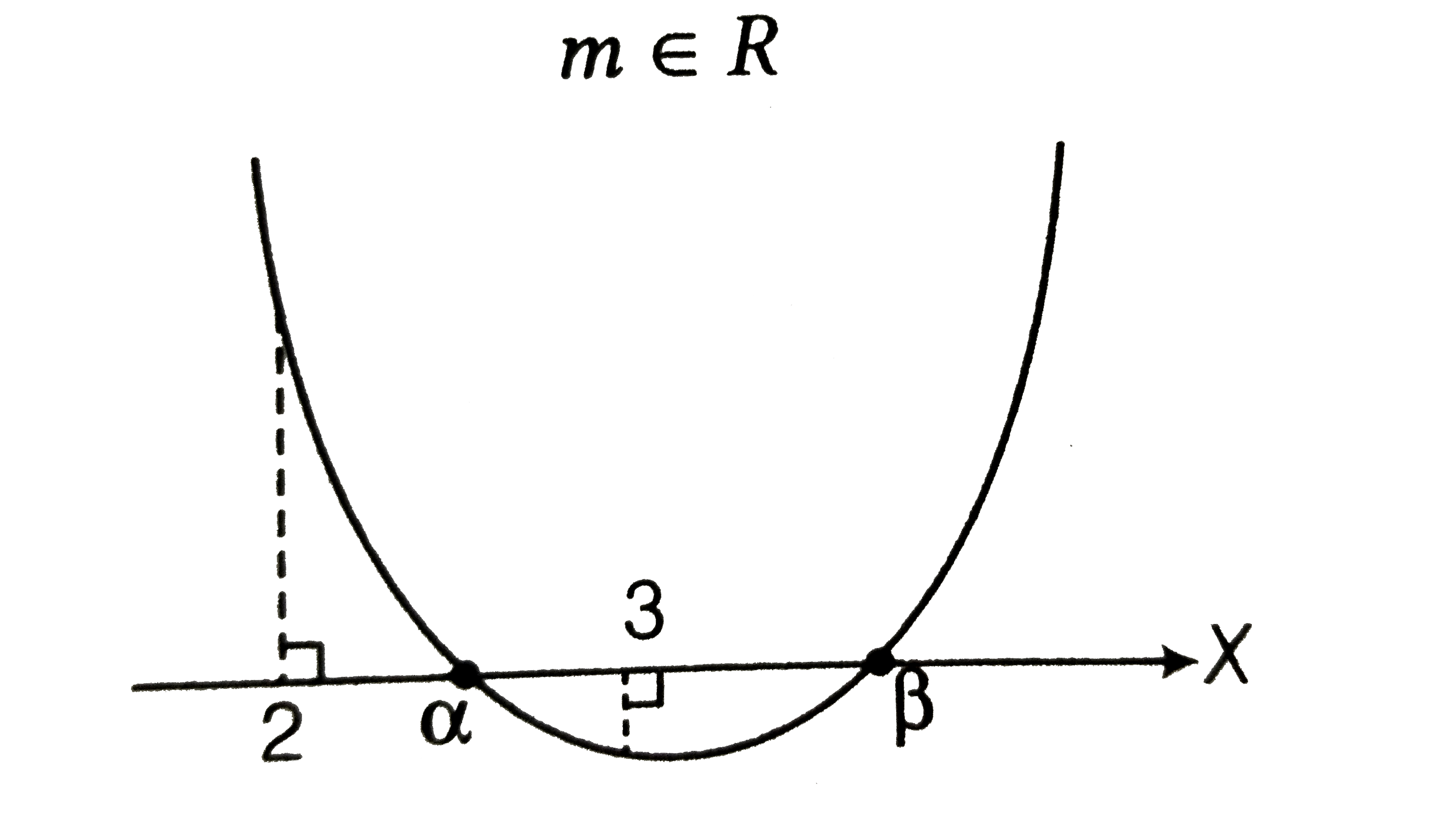
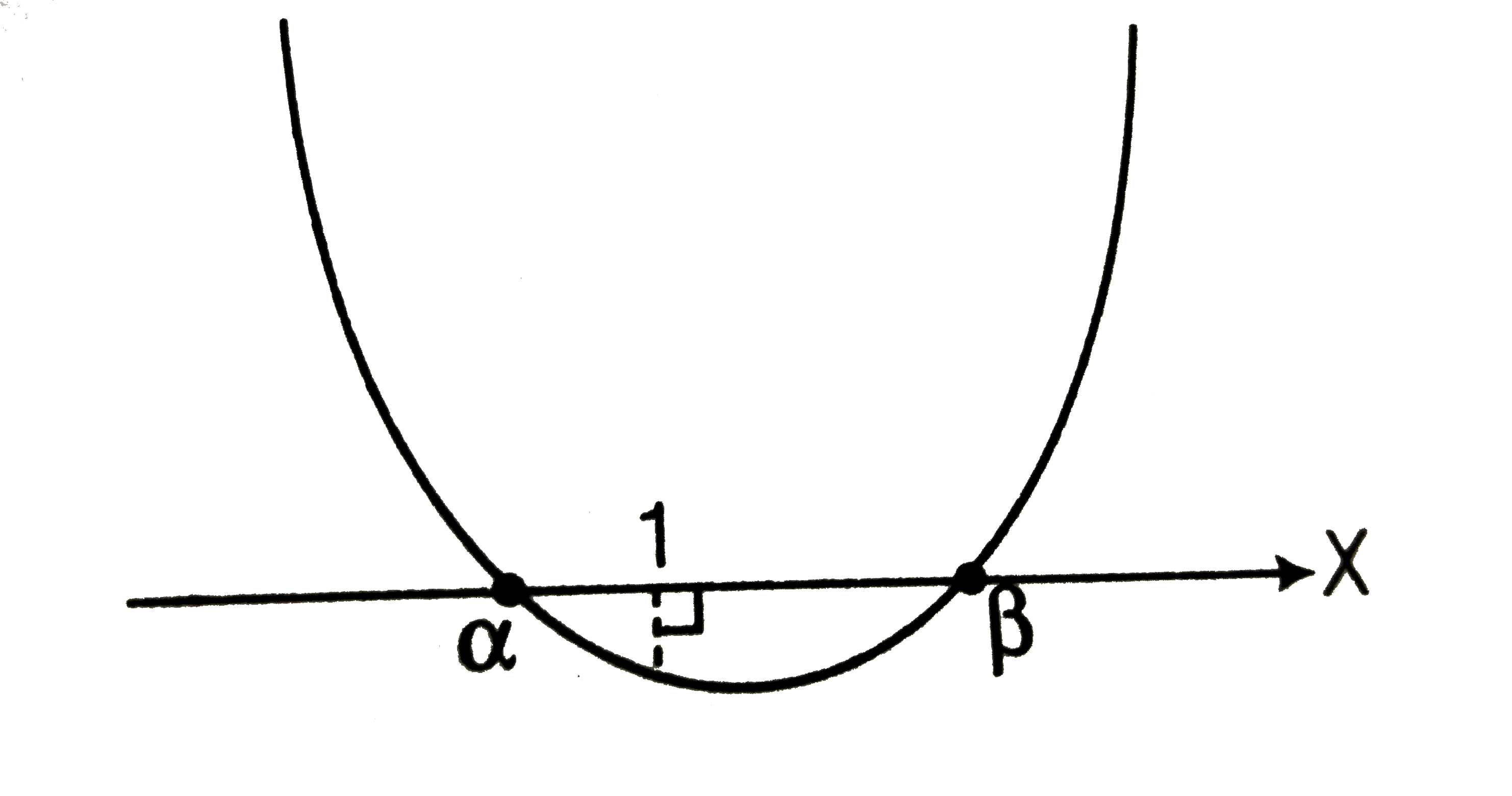
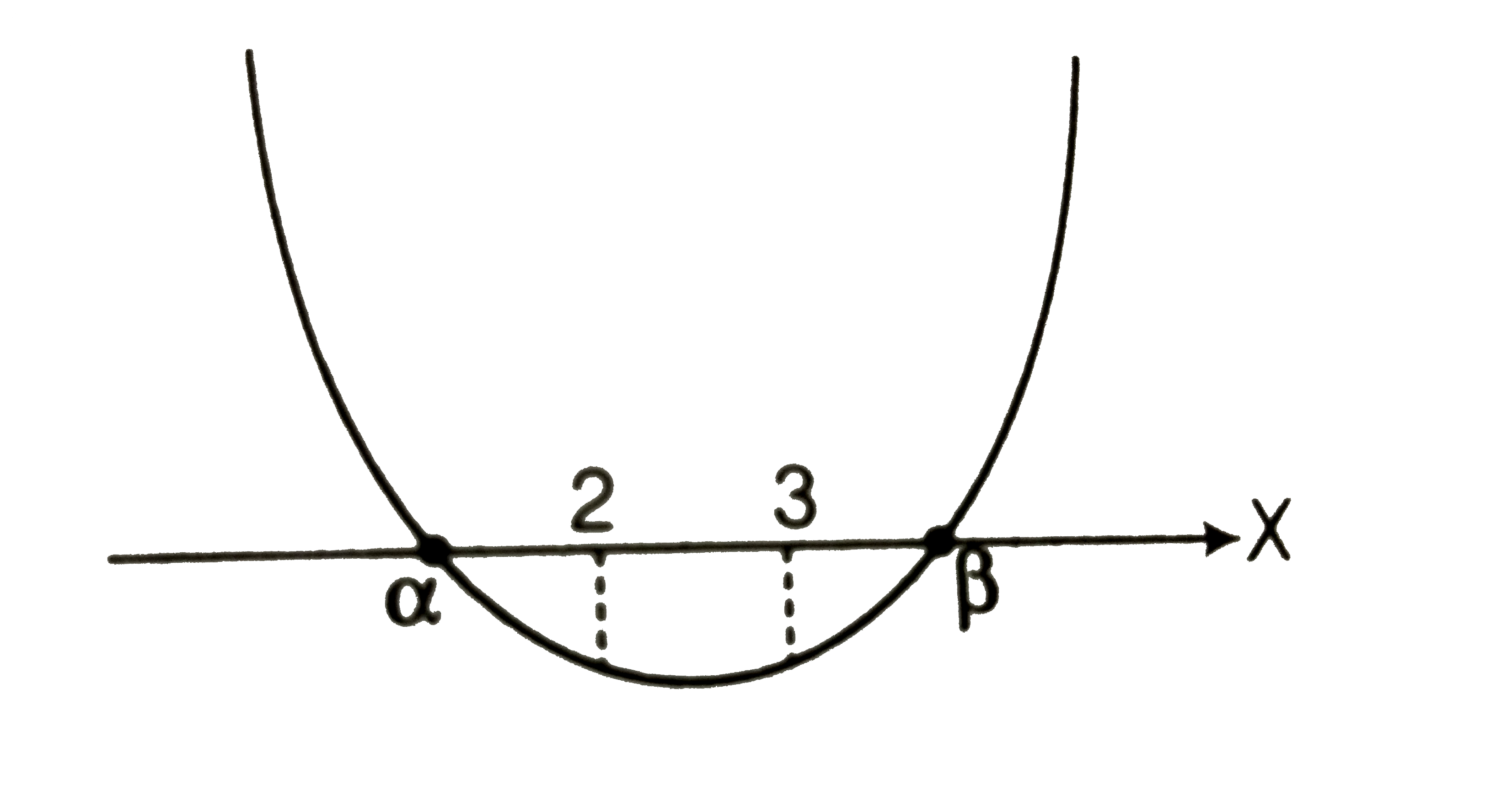
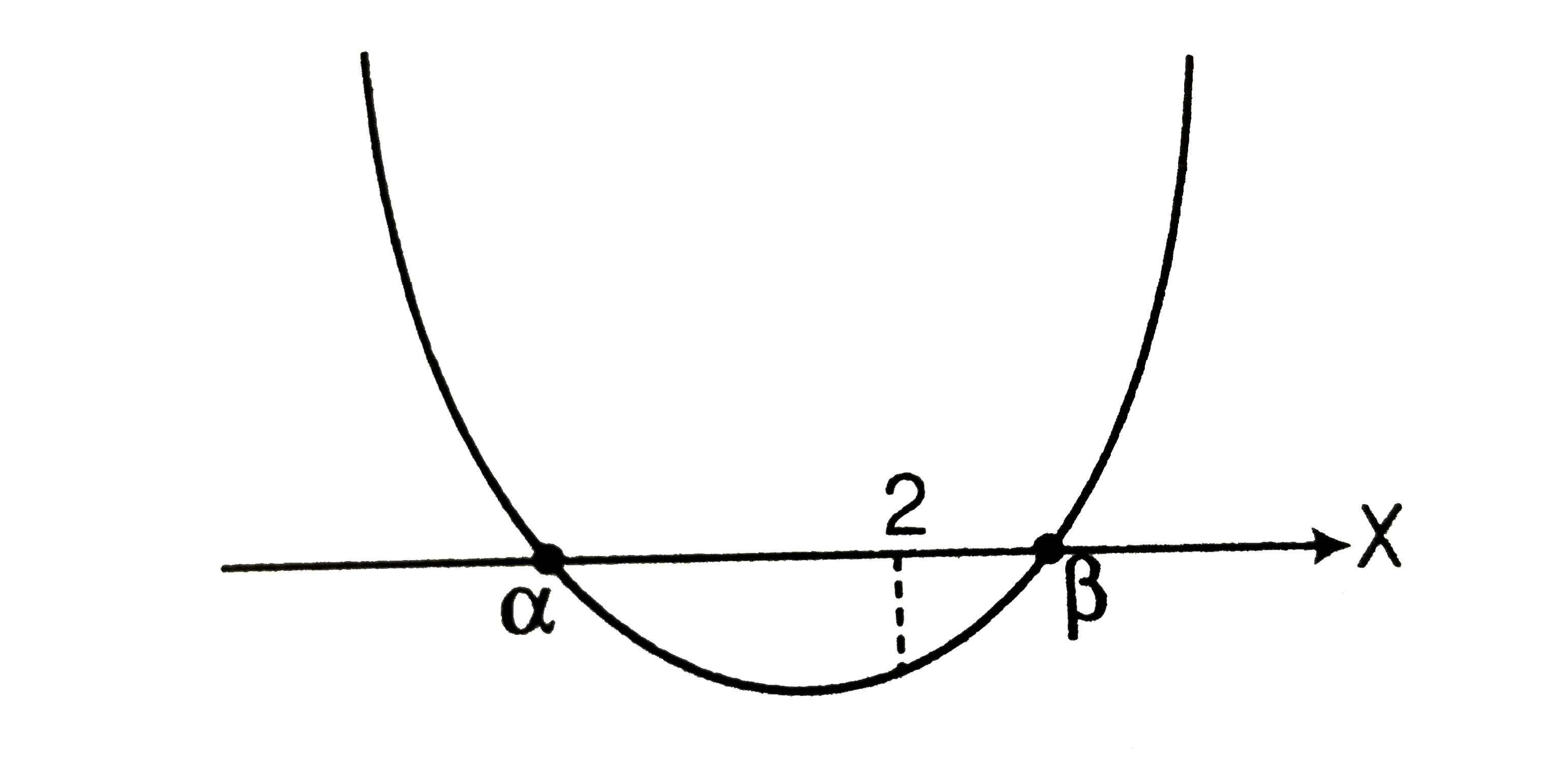
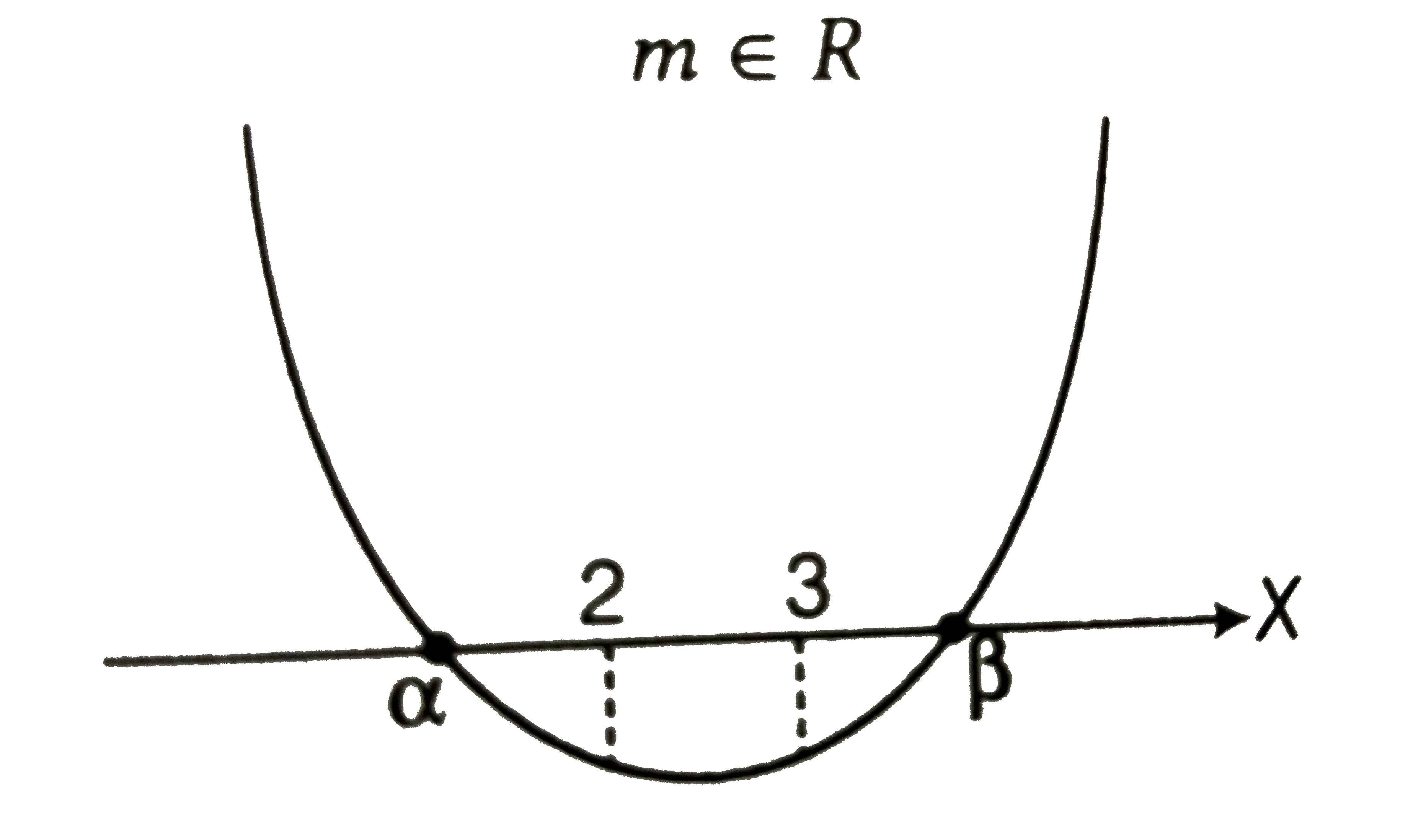
- For what values of m the equation (1+m)x^(2)-2(1+3m)x+(1+8m)=0 has (m ...
Text Solution
|
- Find the cube of (2a-3b)
Text Solution
|
- If r is the ratio of the roots of the equation ax^2 + bx + c = 0 , sho...
Text Solution
|
- If the roots of the equation 1/ (x+p) + 1/ (x+q) = 1/r are equal in ma...
Text Solution
|
- If one root of the equation ax^2 + bx + c = 0 is equal to the n^(th) p...
Text Solution
|
- If alpha, beta be the roots of the equation ax^2 + bx + c= 0 and gamma...
Text Solution
|
- Show that the roots of the equation (a^(2)-bc)x^(2)+2(b^(2)-ac)x+c^(2)...
Text Solution
|
- If the equation x^(2)-px+q=0 and x^(2)-ax+b=0 have a comon root and th...
Text Solution
|
- If the equation x^(2)-2px+q=0 has two equal roots, then the equation (...
Text Solution
|
- Solve the equation x^(log(x)(x+3)^(2))=16.
Text Solution
|
- Solve the equation (2+sqrt(3))^(x^(2)-2x+1)+(2-sqrt(3))^(x^(2)-2x-1)=...
Text Solution
|
- Solve the equation x^(2)+(x/(x-1))^(2)=8
Text Solution
|
- Find number of solutions of the equation sqrt((x+8)+2sqrt(x+7))+sqrt((...
Text Solution
|
- Find value of x if x^2+5|x|+6=0
Text Solution
|
- Solve x^(2)+2x-3
Text Solution
|
- Solve the system x^(2)-2|x|=0
Text Solution
|
- If alpha, beta, gamma are the roots of the cubic x^(3)-px^(2)+qx-r=0 ...
Text Solution
|
- If A(1),A(2),A(3),...,A(n),a(1),a(2),a(3),...a(n),a,b,c in R show that...
Text Solution
|
- One root of the quadratic equation x^(2)-12x+a=0 is thrice the other....
Text Solution
|
- If [x] is the integral part of a real number x. Then solve [2x]-[x+1]=...
Text Solution
|