Home
Class 12
MATHS
The complex numbers z = x + iy which sat...

The complex numbers z = x + iy which satisfy the equation `|(z-5i)/(z+5i)|=1`, lie on

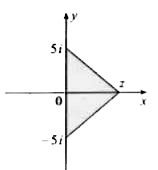
Text Solution

Verified by Experts

The correct Answer is:
T
Promotional Banner

Topper's Solved these Questions

  • COMPLEX NUMBERS

    ML KHANNA|Exercise Problem Set (1) (True and False)|5 Videos

  • COMPLEX NUMBERS

    ML KHANNA|Exercise Problem Set (2) (M.C.Q)|111 Videos

  • CO-ORDINATE GEOMETRY OF THREE DIMENSION

    ML KHANNA|Exercise SELF ASSIGNMENT TEST |11 Videos

  • CONCEPTS OF SET THEORY

    ML KHANNA|Exercise Self Assessment Test|13 Videos

Similar Questions

Explore conceptually related problems

The complex number z which satisfy the equations |z|=1 and |(z-sqrt(2)(1+i))/(z)|=1 is: (where i=sqrt(-1) )

The complex number z satisfying the equation |z-i|=|z+1|=1

The complex number z which satisfies the condition |(i +z)/(i-z)|=1 lies on:

The number of complex number z satisfying the equations |z|-4=|z-i|-|z+5i|=0 is

All complex numbers 'z' which satisfy the relation |z-|z+1||=|z+|z-1|| on the complex plane lie on the

If complex number z=x +iy satisfies the equation Re (z+1) = |z-1| , then prove that z lies on y^(2) = 4x .