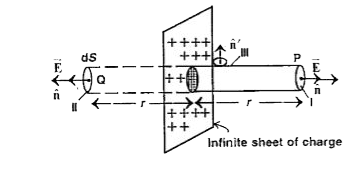
Text Solution
Verified by Experts
Topper's Solved these Questions
GAUSS'S THEOREM
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED NUMERICALS|4 VideosGAUSS'S THEOREM
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS|8 VideosFORCE ON A CURRENT
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS|10 VideosHUYGENS' PRINCIPLE
BETTER CHOICE PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS |11 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-GAUSS'S THEOREM-LONG ANSWER TYPE QUESTIONS
- State Gauss' law and using this law , derive an expression for the ele...
Text Solution
|
- Derive expression for the electric field due to a uniformly charged sp...
Text Solution
|
- State Gauss's theorem with the help of diagram, derive an expression f...
Text Solution
|
- State Gauss's theorem with the help of diagram, derive an expression f...
Text Solution
|
- State Gauss' theorem in electrostatics. Using it, derive an expression...
Text Solution
|
- State Gauss' theorem in electrostatics. Derive an expression for the e...
Text Solution
|
- State Gauss' theorem in electrostatics. Derive an expression for the e...
Text Solution
|
- State Gauss' theorem in electrostatics. Using it, derive an expression...
Text Solution
|
- State Gauss' theorem in electrostatics. Derive an expression for the e...
Text Solution
|