Text Solution
Verified by Experts
Topper's Solved these Questions
CAPACITANCE
BETTER CHOICE PUBLICATION|Exercise LONG ANSWERTYPE QUESTIONS (5/6 Marks Questions) |16 VideosCAPACITANCE
BETTER CHOICE PUBLICATION|Exercise NUMERICAL PROBLEMS |21 VideosCAPACITANCE
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)|5 VideosALTERNATING CURRENTS
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS|11 VideosCLASSIFICATION OF MATERIALS
BETTER CHOICE PUBLICATION|Exercise Most expected question (2 marks)|3 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-CAPACITANCE -SHORT ANSWER TYPE QUESTIONS (3/4 MARKS QUESTIONS)
- Derive an expression for energy density of a parallel plate capacitor.
Text Solution
|
- Obtain the expression for the energy stored in a capacitor connected a...
Text Solution
|
- Give the expression for the energy stored in a capacitor and an indica...
Text Solution
|
- What is a parallel plate capacitor? Derive an expression for the capac...
Text Solution
|
- What is a parallel plate capacitor? Derive an expression for the capac...
Text Solution
|
- Derive an expression for capacitance of a parallel plate capacitor.
Text Solution
|
- Derive an expression for the capacitance of a parallel plate capacitor...
Text Solution
|
- What is capacitor? Explain its principle.
Text Solution
|
- Three capacitors of capacitance C1,C2andC3 are connected in parallel. ...
Text Solution
|
- Derive expression for the total resistance of a circuit in which a few...
Text Solution
|
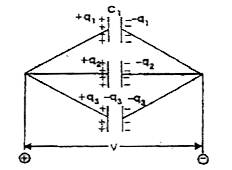
- Three capacitors C1, C2, C3 are Connected in series. Derive an express...
Text Solution
|