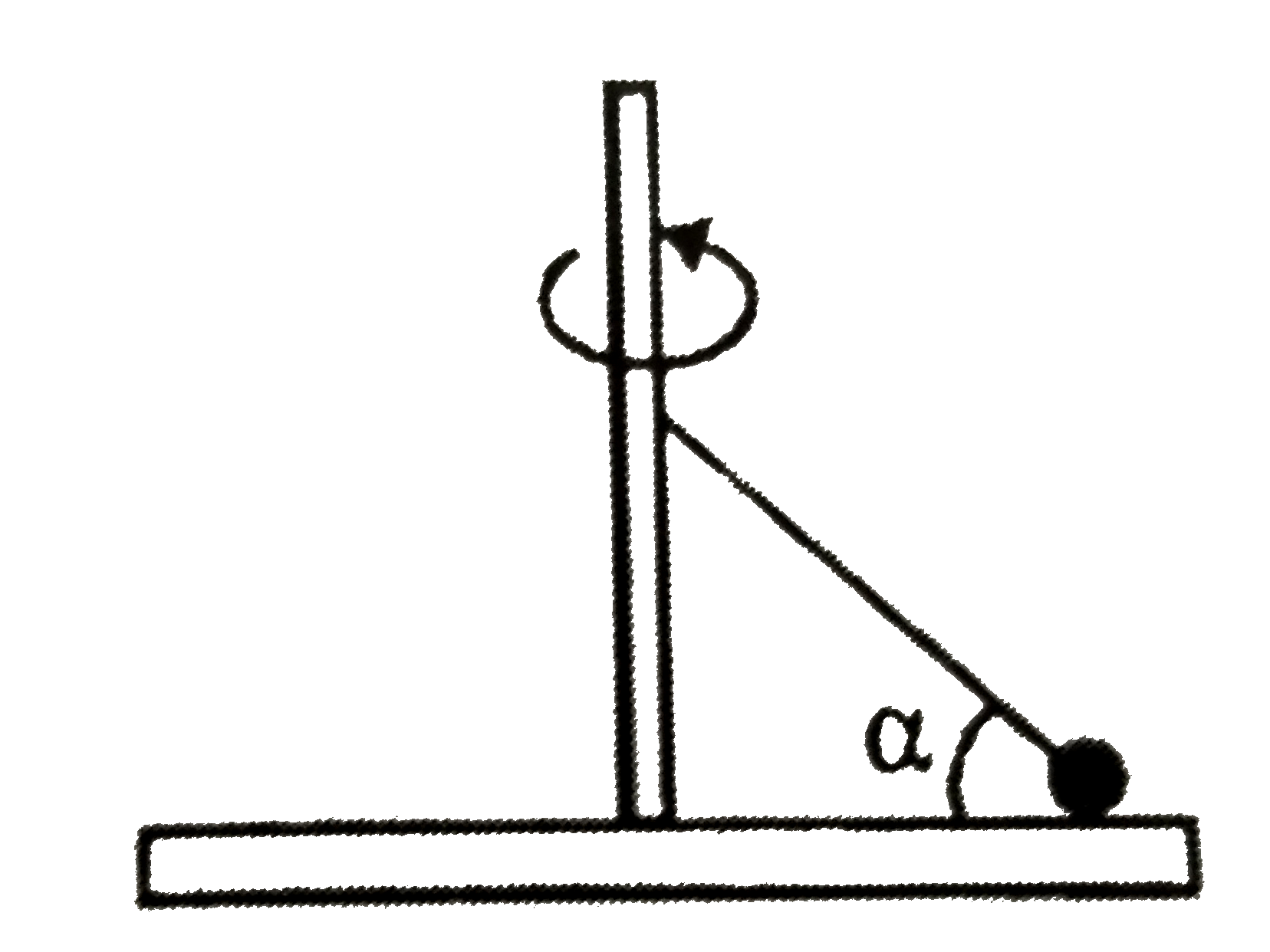
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-CIRCULAR MOTION-Dynamics of circular motion
- The ball of mas m moves with speed v againest a smooth , fixed vertica...
Text Solution
|
- A crystal speeding at 18 km/h on a level road takes a sharp circular t...
Text Solution
|
- A stone of mass 0.25 kg tied to the end of a string is whirled round ...
Text Solution
|
- A circular platform rotates around a vertical axis with angular veloci...
Text Solution
|
- An aircraft executes a horizontal loop at a speed of 720km h^(-1) with...
Text Solution
|
- A block of mass m = 20 kg is kept is a distance R = 1m from central ax...
Text Solution
|