Home
Class 12
PHYSICS
In the figure masses m(1),m(2) and M are...

In the figure masses `m_(1),m_(2)` and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between `m_(1)` and M and that between `m_(2)` and ground is `0.3.` The pulleys and the string are massless. The string is perfectly horizontal between `P_(1) and m_(1)` and also between `P_(2) and m_(2).` The string is perfectly verticle between `P_(1) and P_(2).` An externam horizontal force F is applied to the mass M. Take `g=10m//s^(2).`

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between `m_(1)` and M be `f_(1)` and that between `m,_(2)` and ground be `f_(2).` For a particular F it is found that `f_(1)=2f_(2).` Find `f_(1) and f_(2).` Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.

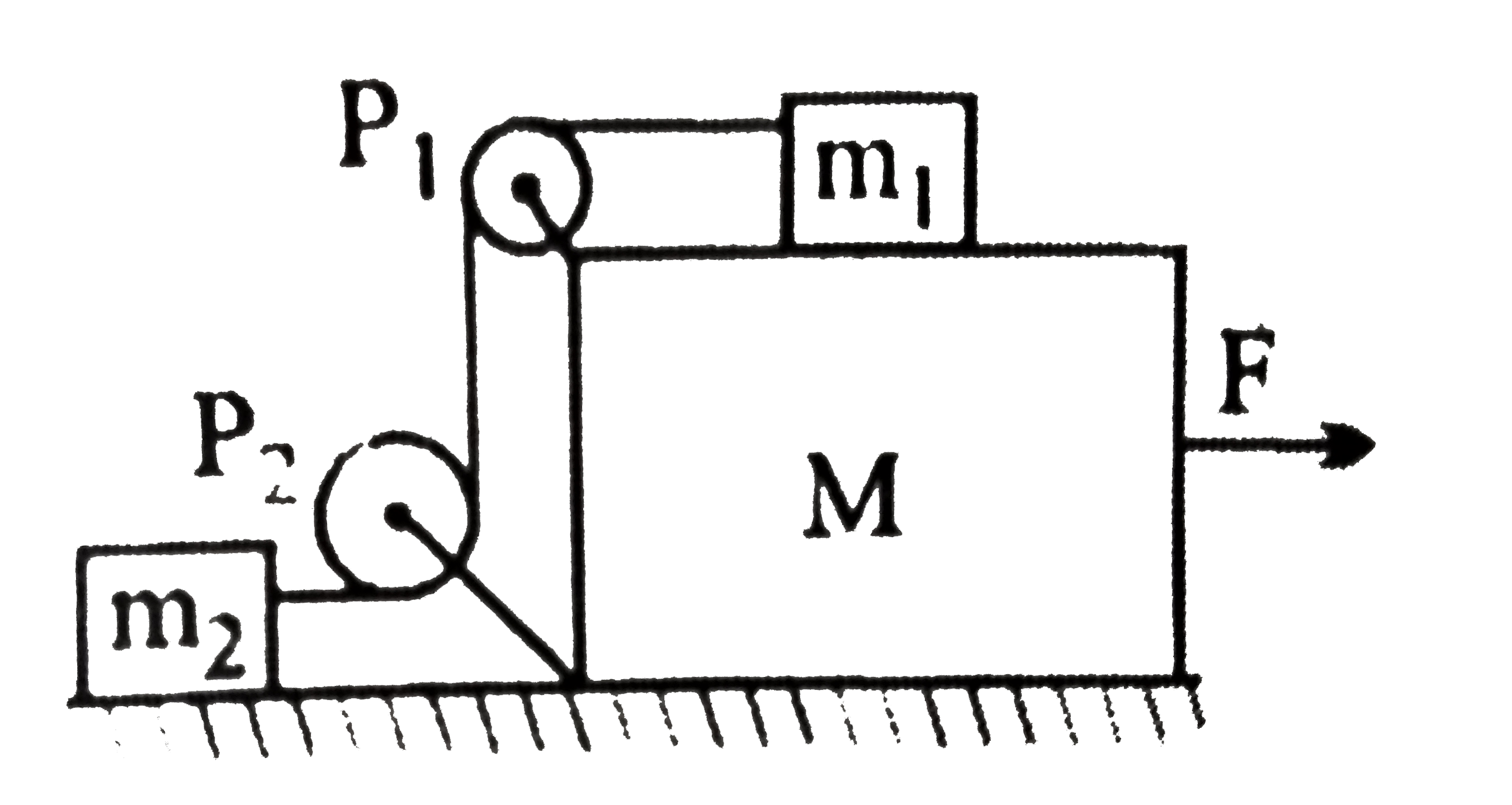
Text Solution

Verified by Experts

The correct Answer is:
`(##ALN_NC_PHY_NLMF_E02_008_A01##)`
(ii) `a=3//5m//s^(2),T=18N,F=60N`
Promotional Banner

Topper's Solved these Questions

  • NEWTON'S LAWS OF MOTION & FRICTION

    ALLEN|Exercise EXERCISE (O-1)|51 Videos

  • NEWTON'S LAWS OF MOTION & FRICTION

    ALLEN|Exercise EXERCISE (O-2)|31 Videos

  • NEWTON'S LAWS OF MOTION & FRICTION

    ALLEN|Exercise EXERCISE (S-1)|23 Videos

  • MOTION IN A PALNE

    ALLEN|Exercise SOLVED EXAMPLE|28 Videos

  • NEWTONS LAWS OF MOTION

    ALLEN|Exercise EXERCISE-III|28 Videos

Similar Questions

Explore conceptually related problems

In the figure masses m_1 , m_2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m_1 and M and that between m_2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P_1 and m_1 and also between P_2 and m_2 . The string is perfectly vertical between P_1 and P_2 . An external horizontal force F is applied to the mass M. Take g=10m//s^2 . (a) Draw a free body diagram for mass M, clearly showing all the forces. (b) Let the magnitude of the force of friction between m_1 and M be f_1 and that between m_2 and ground be f_2 . For a particular F it is found that f_1=2f_2 . Find f_1 and f_2 . Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.

In the figure masses m_1 , m_2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m_1 and M and that between m_2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P_1 and m_1 and also between P_2 and m_2 . The string is perfectly vertical between P_1 and P_2 . An external horizontal force F is applied to the mass M. Take g=10m//s^2 . (a) Draw a free body diagram for mass M, clearly showing all the forces. (b) Let the magnitude of the force of friction between m_1 and M be f_1 and that between m_2 and ground be f_2 . For a particular F it is found that f_1=2f_2 . Find f_1 and f_2 . Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.

When force F applied on m_(1) and there is no friction between m_(1) and surface and the coefficient of friction between m_(1)and m_(2) is mu. What should be the minimum value of F so that there is on relative motion between m_(1) and m_(2)

In fig. both pulleys and the string are massless and all the surfaces are frictionless. Given m_(1)=1kg, m_(2)= 2kg, m_(3)=3kg . Find the tension in the string

In the adjacent figure, masses of A,B and C are 1kg ,3kg and 2kg respectively. Find (a) the acceleration of the system and (b) tension in the strings. Neglect friction. (g=10m//s^(2))

If coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m//s^(2))

Two blocks of masses m_(1) and m_(2) are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m_(1) and platform is 2mu and that between block m_(2) and platform is mu .The platform moves with an acceleration a . The normal reation between the blocks is

In fig. both pulleys and the string are massless and all the surfaces are frictionless. Given m_(1)=1kg, m_(2)= 2kg, m_(3)=3kg . The acceleration of m_(1) is

In fig. both pulleys and the string are massless and all the surfaces are frictionless. Given m_(1)=1kg, m_(2)= 2kg, m_(3)=3kg . The acceleration of m_(3) is

As shown in the figure, M is a man of mass 60 kg standing on a block of mass 40 kg kept on ground. The co-efficient of friction between the feet of the man and the block is 0.3 and that between B and the ground is 0.1. If the man accelerates with an acceleration 2(m)/(s^2) in the forward direction, then,