Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-BASIC MATHEMATICS USED IN PHYSICS &VECTORS -EXERCISE-IV ASSERTION & REASON
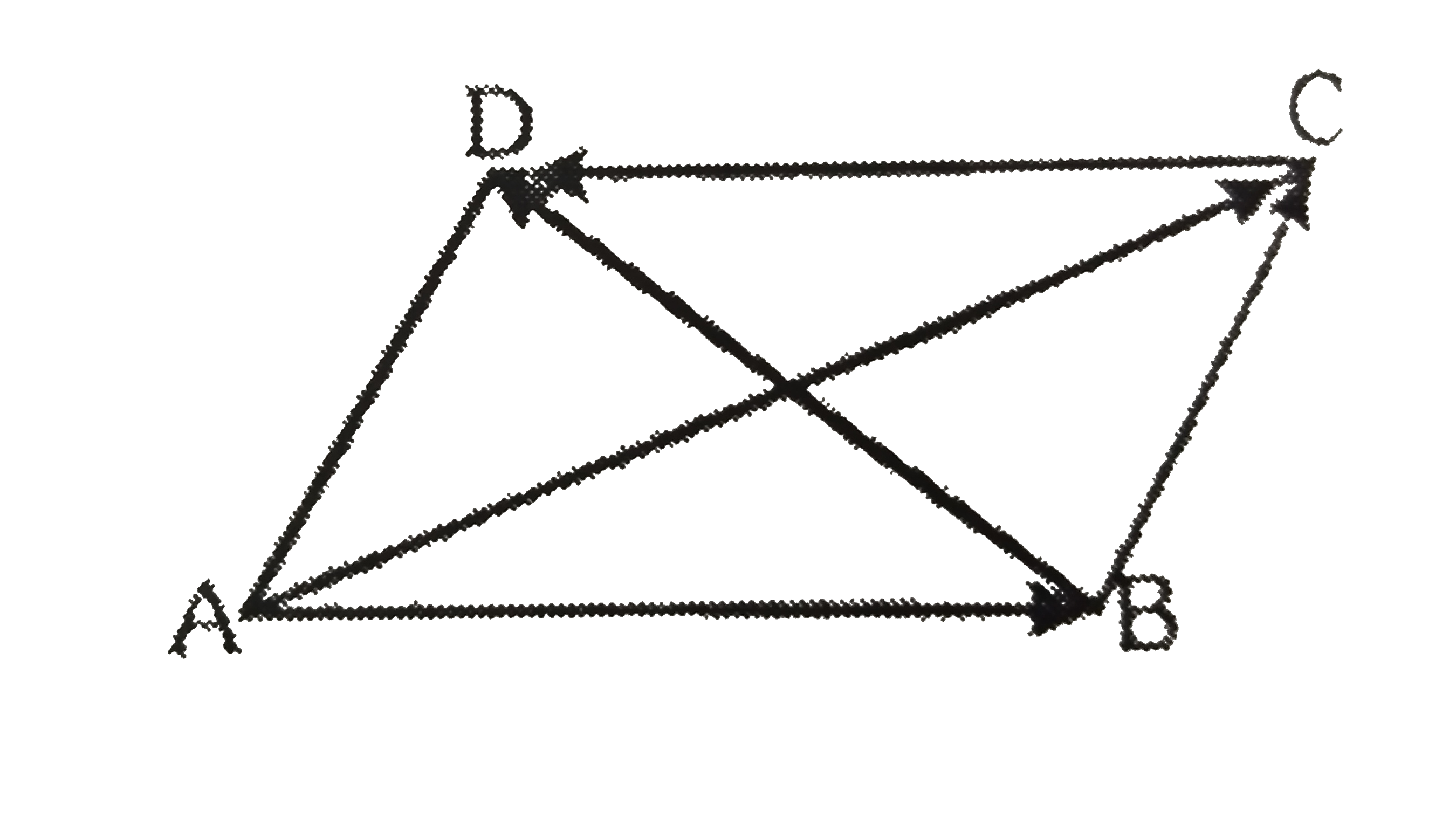
- In a parallelogram ABCD. Prove that vec(AC)+ vec (BD) = 2 vec(BC)
Text Solution
|
- Statement-I : If the initial and final positions coincide, the displac...
Text Solution
|
- Assertion: A vector qunatity is a quantity that has both magnitude and...
Text Solution
|
- Assertion: The direction of a zero (nu)) vector is indeterminate. Re...
Text Solution
|
- Assertion: A vector can have zero magnitude if one of its components i...
Text Solution
|
- Assertion: The angle between the two vectors (hati+hatj) and (hatj+hat...
Text Solution
|
- Assertion: Distance is a scalar quantity. Reason: Distance is the le...
Text Solution
|
- Assertion : The sum of squares of cosines of angles made by a vector ...
Text Solution
|
- Assertion: Adding a scalar to a vector of the same dimensions is a mea...
Text Solution
|
- Assertion: The dot product of one vector with another vector may be sc...
Text Solution
|
- Assertion: A physical quantity can be regarded as a vector, if magnitu...
Text Solution
|
- Assertion: Vecot (hati+hatj+hatk) is perpendicular to (hati-2hatj+hatk...
Text Solution
|