A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ML KHANNA-FUNCTIONS-SELF ASSESSMENT TEST
- Let g(x)=1+x-[x] and Then for all x,f {g(x)} is equal to
Text Solution
|
- If f (x + ay , x - ay) = axy , then f(x,y) is equal to
Text Solution
|
- A functions from the set of natural numbers to integers defined by
Text Solution
|
- The domain of sin ^(-1)[log (3) ((x)/(3)) ] is
Text Solution
|
- The function f(x)=log(x+sqrt(x^(1)+1)) is
Text Solution
|
- Let g(x)=1+x-[x] and f(x)={(-1",",x lt 0),(0",",x=0),(1",",x gt 0):}, ...
Text Solution
|
- If f(x)=(a-x^(n))^(1//n) where a gt 0 and n in N , then f[f(x)] is equ...
Text Solution
|
- Let f be a real-valued function on the interval (-1,1) such that e^(-x...
Text Solution
|
- Let f(x)=x^2a n dg(x)=sinxfora l lx in Rdot Then the set of all x sat...
Text Solution
|
- The function f:[0,3] to [1,29], defined by f(x)=2x^(3)-15x^(2)+36x+1 i...
Text Solution
|
- The real number k for which the equation 2x^3 + 3x +k=0 has two distin...
Text Solution
|
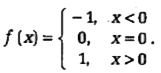 Then for all x,f {g(x)} is equal to
Then for all x,f {g(x)} is equal to