Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
JEE MAINS PREVIOUS YEAR-JEE MAINS 2021-Physics (Section B )
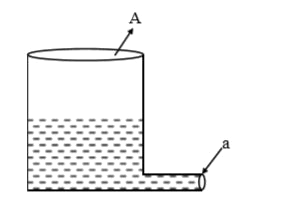
- A light cylindrical vessel is kept on a horizontal surface. Area of ba...
Text Solution
|
- If the maximum value of accelerating potential provided by a radio fre...
Text Solution
|
- An object is placed at a distance of 12 cm from a convex lens. A conve...
Text Solution
|
- For the given circuit, the power across zener diode is mW.
Text Solution
|
- The acceleration due to gravity is found upto an accuracy of 4% on a p...
Text Solution
|
- A circular coil of radius 8.0 cm and 20 turns is rotated about its ver...
Text Solution
|
- A source of light is placed in front of a screen. Intensity of light o...
Text Solution
|
- A coil in the shape of an equilateral triangle of side 10 cm lies in a...
Text Solution
|
- Two waves are simultaneously passing through a string and their equati...
Text Solution
|
- Two simple harmonic motions are represented by the equations x1=5sin(2...
Text Solution
|
- The coefficient of static friction between two blocks is 0.5 and the t...
Text Solution
|