Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
BETTER CHOICE PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS|8 VideosELECTROMAGNETIC INDUCTION
BETTER CHOICE PUBLICATION|Exercise MOST EXPECTED QUESTIONS |9 VideosELECTROMAGNETIC INDUCTION
BETTER CHOICE PUBLICATION|Exercise SHORT ANSWER TYPE QUESTIONS|10 VideosELECTRICAL MEASUREMENTS
BETTER CHOICE PUBLICATION|Exercise Most Expected Questions|7 VideosELECTROMAGNETIC WAVES
BETTER CHOICE PUBLICATION|Exercise NUMERICALS|4 Videos
Similar Questions
Explore conceptually related problems
BETTER CHOICE PUBLICATION-ELECTROMAGNETIC INDUCTION-SHORT ANSWERTYPE QUESTIONS
- What is Lenz's law? prove that Lenz's law is in accordance with the co...
Text Solution
|
- Explain the phenomenon of self induction?
Text Solution
|
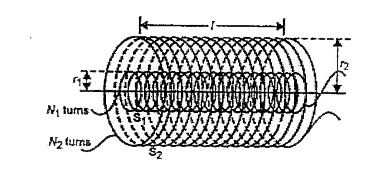
- What is meant by mutual induction? Define coefficient of mutual induct...
Text Solution
|
- What are eddy currents ?
Text Solution
|
- State Lenz’s law.Give one example to illustrate it.
Text Solution
|
- State and explain Faraday’s law of electromagnetic induction.
Text Solution
|
- Define co-efficient of mutual induction and find an expression for it.
Text Solution
|
- Show that Lenz's law obeys the law of conservation of energy.
Text Solution
|
- What is Lenz's law? prove that Lenz's law is in accordance with the co...
Text Solution
|
- Define co-efficient of mutual induction and find an expression for it.
Text Solution
|
- What is meant by mutual induction? Define coefficient of mutual induct...
Text Solution
|
- Show that energy stored in an inductor L, when a current is f establis...
Text Solution
|
- State and explain Lenz's law of electromagnetic induction. Give one ex...
Text Solution
|