Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MTG IIT JEE FOUNDATION-TRIANGLES-NCERT SECTION (Exercise 7.1)
- In quadrilateral ABCD, AC=AD and AB bisects angleA (see figure). Show ...
Text Solution
|
- ABCD is quadrilateral in which AD=BC and angleDAB= angleCBA (see figur...
Text Solution
|
- ABCD is quadrilateral in which AD=BC and angleDAB= angleCBA (see figur...
Text Solution
|
- ABCD is quadrilateral in which AD=BC and angleDAB= angleCBA (see figur...
Text Solution
|
- AD and BC are equal perpendiculars to a line segment AB (see Fig. 7...
Text Solution
|
- l and m are two parallel lines intersected by another pair of paralle...
Text Solution
|
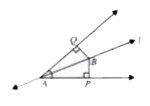
- Line l is the bisector of an angleA and B is any point on I. BP and BQ...
Text Solution
|
- Line l is the bisector of an angleA and B is any point on I. BP and BQ...
Text Solution
|
- In the given figure, AC=AE, AB=AD and angleBAD=angleEAC. Prove that BC...
Text Solution
|
- AB is a line segment D and P is its mid-point. D and E are points on t...
Text Solution
|
- AB is a line segment and P is its mid-point. D and E are points on the...
Text Solution
|
- In right triangle ABC, right angled at C, Mis the mid-point of hypoten...
Text Solution
|
- In right triangle ABC, right angled at C, Mis the mid-point of hypoten...
Text Solution
|
- In right triangle ABC, right angled at C, Mis the mid-point of hypoten...
Text Solution
|