Home
Class 9
PHYSICS
The line that joins the saturn to the su...

The line that joins the saturn to the sun sweeps area `A_(1), A_(2)` and `A_(3)` in time intervals of `6` weeks, `3` weeks and `2` weeks respectively as shows in the Fig. What is the correct relation between `A_(1), A_(2)` and `A_(3)`?

Text Solution

Verified by Experts

According to Kepler.s second law, the areal velocity of the planet around the Sun is constant
Therefore ,
`A_(1) gt A_(2) gt A_(3) and A_(1) = 2 A_(2), A_(1) = 3 A_(3)`
Promotional Banner

Topper's Solved these Questions

  • FOOTSTEPS TOWARDS CBSE BOARD

    MTG IIT JEE FOUNDATION|Exercise Section - D |14 Videos

  • FOOTSTEPS TOWARDS CBSE BOARD

    MTG IIT JEE FOUNDATION|Exercise Section - B|12 Videos

  • FOOTSTEPS TOWARDS JEE MAIN

    MTG IIT JEE FOUNDATION|Exercise Section B (Numerical Value Type Questions)|10 Videos

  • FOOTSTEPS TOWARDS NEET

    MTG IIT JEE FOUNDATION|Exercise Multiple Choice Question|45 Videos

Similar Questions

Explore conceptually related problems

Make the constraint relation between a_(1),a_(2) and a_(3)

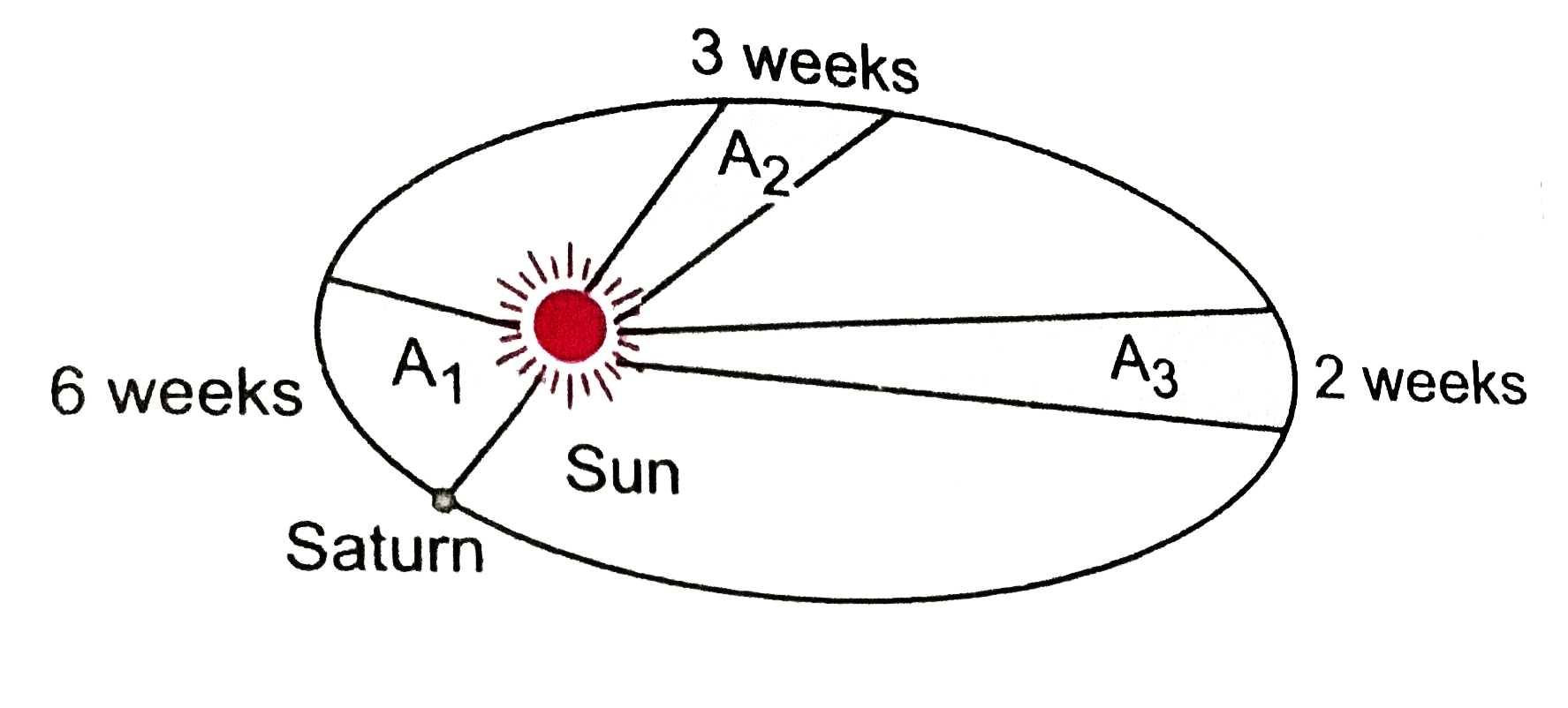
In Fig. the line that join a planet to the sun sweep out areas A_(1),A_(2),A_(3) in time intervals 6 weeks, 3 weeks and 2 weeks respectively. How are A_(1),A_(2),A_(3) ?realted

A planet moving around the sun sweeps area A_(1) in 2 days, A_(2) in 4 days and A_(3) in 9 days. Then, relation between them

A planet moving around sun sweeps area A_(1) in 2 days, A_(2) in 3 days and A_(3) in 6 days, then find the relation between A_(1),A_(2) and A_(3)

If A_(1),A_(2),A_(3) denote respectively the areas of an inscribed polygon of 2n sides , inscribed polygon of n sides and circumscribed poylgon of n sides ,then A_(1),A_(2),A_(3) are in

If a_(n) = 3-4n , then what is a_(1)+a_(2)+a_(3)+…+a_(n) equal to ?

If a_(1),a_(2),a_(3) are the last three digits of 17^(256) respectively then the value of a_(2)-a_(1)-a_(3) is equal

An equivalence relation R in A divides it into equivalence classes A_(1),A_(2), A_(3) . What is the value of A_(1)uu A_(2)uu A_(3) and A_(1)nn A_(2)nn A_(3)

If A,A_(1),A_(2) and A_(3) are the areas of the inscribed and escribed circles of a triangle, prove that (1)/(sqrt(A))=(1)/(sqrt(A_(1)))+(1)/(sqrt(A_(2)))+(1)/(sqrt(A_(3)))