Home
Class 12
MATHS
A 10 inches long pencil AB with mid poin...

A 10 inches long pencil AB with mid pointC and a small eraser P are placed on the horizontal top of a table such that PC = `sqrt5` inches and `angle`PCB = `tan^ (- 1) (2)`. The acute angle through which the pencil must be rotated about C so that the perpendicular distance between eraser and pencil becomes exactly 1 inch is :

A

`tan^(-1) (1)`

B

`tan^(-1) (3/5)`

C

`tan^(-1) (4/3)`

D

`tan^(-1) (1/2)`

Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • JEE MAINS 2021

    JEE MAINS PREVIOUS YEAR|Exercise Mathematics (Section B)|50 Videos

  • JEE MAINS 2020

    JEE MAINS PREVIOUS YEAR|Exercise MATHEMATICS|250 Videos

  • JEE MAINS 2022

    JEE MAINS PREVIOUS YEAR|Exercise MATHEMATICS (SECTION - B)|10 Videos

Similar Questions

Explore conceptually related problems

A rod P of length 1 m, is hinged at one end A there is a ring attached to the other end. Another long rod Q is hinged at B and it passes through the ring. The rod P is rotated about an axis which is perpendicular to the plane is which both rods are present and the variations between the angles theta and phi are plotted as shown. The distance between the hinges A and B is

A 100 turn closely wound circular coil of radius 10cm carries a current of 3*2A . (i) What is the field at the centre of the coil? (ii) What is the magnetic moment of this arrangement? The coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A uniform magnetic field of 2T in the horizontal direction exists such that initially the axis of the coil is in the direction of the field. The coil rotates through an angle of 90^@ under the influence of the magnetic field. (iii) What are the magnitudes of the torques on the coil in the initial and final positions? (iv) What is the angular speed acquired by the coil when it has rotated by 90^@ ? The moment of inertia of the coil is 0*1kgm^2 .

A long conducting wire is placed along Y-axis and a current of 5 A is flowing through it in positive Y-axis. A charged particle of charge + 3.2 xx 10^(-19) C is moving parallel to the conductor towards negative Y-axis with a speed of 5 xx 10^(4) m s^(-1) . Calculate the force exerted by the magnetic field of current on charged particle. The perpendicular distance between charged particle and wire is 25 cm.

Two particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is mu (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (omega) of platfrom about it center so that the blocks remain stationery relative to platform. (If mu=(1)/(sqrt(2)) , r=2.5m and g=10m//s^(2) )

A uniform rod AB of mass m and length 5a is free to rotate on a smooth horizontal table about a pivot through P, a point on AB such that AP = a. A particle of mass 2m moving on the table strikes AB perpendicularly at the point 2a from P with speed v, the rod being at rest. If the coefficient of restitution between them is (1)/( 4) , find their speeds immediately after impact.

Two blocks of mass m_(1)=10kg and m_(2)=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m_(1) is 0.5 while there is no friction between m_(2) and the table. the table is rotating with an angular velocity of 10rad//s . about a vertical axis passing through its center O . the masses are placed along the diameter of the table on either side of the center O such that the mass m_(1) is at a distance of 0.124m from O . the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m//s^(2)) . (a) Calculate the friction on m_(1) (b) What should be the minimum angular speed of the turntable so that the masses will slip from this position? (c ) How should the masses be placed with the string remaining taut so that there is no friction on m_(1) .

An infinitely long straight conductor and a flat rectangular contour with sides a and b and with N turns lie in a single plane. The distance between the straight conductor and the side of the contour closest to the straight conductor is c. Determine the following quantities: (1) the mutual inductance of the conductor and the contour, (2) the quantity of electricity induced in the contour if the contour is rotated through 90^@ about the AB axis provided that a current I is flowing in the contour and the resistance of the contour is R, (3) the work that must be done to rotate the contour through 1800 about the AB axis provided that there is current I both in the long conductor and in the contour and that the sense of the current in the contour is clockwise (in the plane of the drawing).

JEE MAINS PREVIOUS YEAR-JEE MAINS 2021-Mathematics (Section A )
  1. Consider the two statements : (S1) : (p to q) vv ( ~ q to p) is a ta...

    Text Solution

    |

  2. A circle C touches the line x = 2y at the point (2, 1) and intersects ...

    Text Solution

    |

  3. The locus of the mid-point of the chords of the hyperbola x^(2)-y^(2)=...

    Text Solution

    |

  4. The domain of the function cosec^(-1)((1+x)/x) is :

    Text Solution

    |

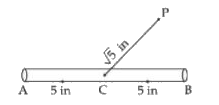
  5. A 10 inches long pencil AB with mid pointC and a small eraser P are pl...

    Text Solution

    |

  6. lim/(x to2)(sum^(9)/(n =1) x/(n(n +1) x^2 +2(2n +1)x + 4))

    Text Solution

    |

  7. Let P be the plane passing through the point (1, 2, 3) and the line of...

    Text Solution

    |

  8. If the value of the integral int0^5 (x + [x])/(e^(x - [x])) dx = alph...

    Text Solution

    |

  9. Let [t] denote the greatest integer less than or equal to t. Let f (...

    Text Solution

    |

  10. Let y(x) be the solution of the differential equation 2x^2dy + (e^y-2x...

    Text Solution

    |

  11. The value of 2 sin (pi/8) sin((2pi)/8) sin((3pi)/8) sin ((5pi)/8) s...

    Text Solution

    |

  12. The value of int(-pi/2)^(pi/2) ((1+sin^(2)x)/(1 +pi^(sinx))) dx is

    Text Solution

    |

  13. Let A = ({:(1,0,0),(0,1,1),(1,0,0):}). Then A^(2025) - A^(2020) is eq...

    Text Solution

    |

  14. A hall has a square floor of dimension 10m xx10 m (see the figure) and...

    Text Solution

    |

  15. The point P(- 2sqrt6, sqrt3) lies on the hyperbola (x^2)/(a^2) - (y^2)...

    Text Solution

    |

  16. The local maximum value of the function f(x)=(2/x)^(x^2),xgt0, is

    Text Solution

    |

  17. A fair die is tossed until six is obtained on it. Let X be the number ...

    Text Solution

    |

  18. If sum(r=1)^(50)tan^(-1)1/(2r^2)=p, then the value of tan p is:

    Text Solution

    |

  19. If (sqrt3 + i)^(100) = 2^(99) (p + iq) , then p and q are roots of the...

    Text Solution

    |

  20. Two fair dice are thrown. The numbers on them are taken as lamda and µ...

    Text Solution

    |