A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MS CHOUHAN-HYDROCARBONS (ALKANES) -LEVEL - 2
Text Solution
|
- Product (A) is :
Text Solution
|
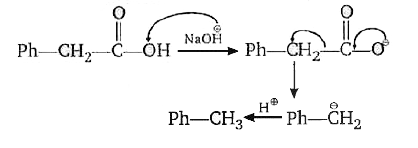
- Ph - CH(2) - overset(O)overset(||)(C) - OH underset((2)H^(oplus))overs...
Text Solution
|
- Match the column I with column II and with column III.
Text Solution
|
- Sum P + Q + R is :
Text Solution
|
- Match the column I and II.
Text Solution
|
- Match the column :
Text Solution
|
- How many distinct monochlorinated products, (including stereoisomers) ...
Text Solution
|
- How many distinct monochlorinated products, (including steroisomers) m...
Text Solution
|
- Match the column :
Text Solution
|
- (x) = total number of di-chloro product
Text Solution
|