Home
Class 10
MATHS
In DeltaABC, AP bot BC, BQ bot AC, B - P...

In `DeltaABC, AP bot BC, BQ bot AC, B - P - C, A- Q - C, ` then prove that `DeltaCPA ~ DeltaCQB.` If AP = 7, BQ = 8, BC = 12, then find AC.

Text Solution

Verified by Experts

The correct Answer is:
AC = 10.5
Promotional Banner

Topper's Solved these Questions

  • SIMILARITY

    BAL BHARTI|Exercise PRACTICE SET 1.4|6 Videos

  • SIMILARITY

    BAL BHARTI|Exercise PROBLEM SET 1 |12 Videos

  • SIMILARITY

    BAL BHARTI|Exercise PRACTICE SET 1.2|5 Videos

  • QUADRATIC EQUATIONS

    BAL BHARTI|Exercise Problem Set - 2 |27 Videos

  • TRIGONOMETRY

    BAL BHARTI|Exercise Problem set 6 |18 Videos

Similar Questions

Explore conceptually related problems

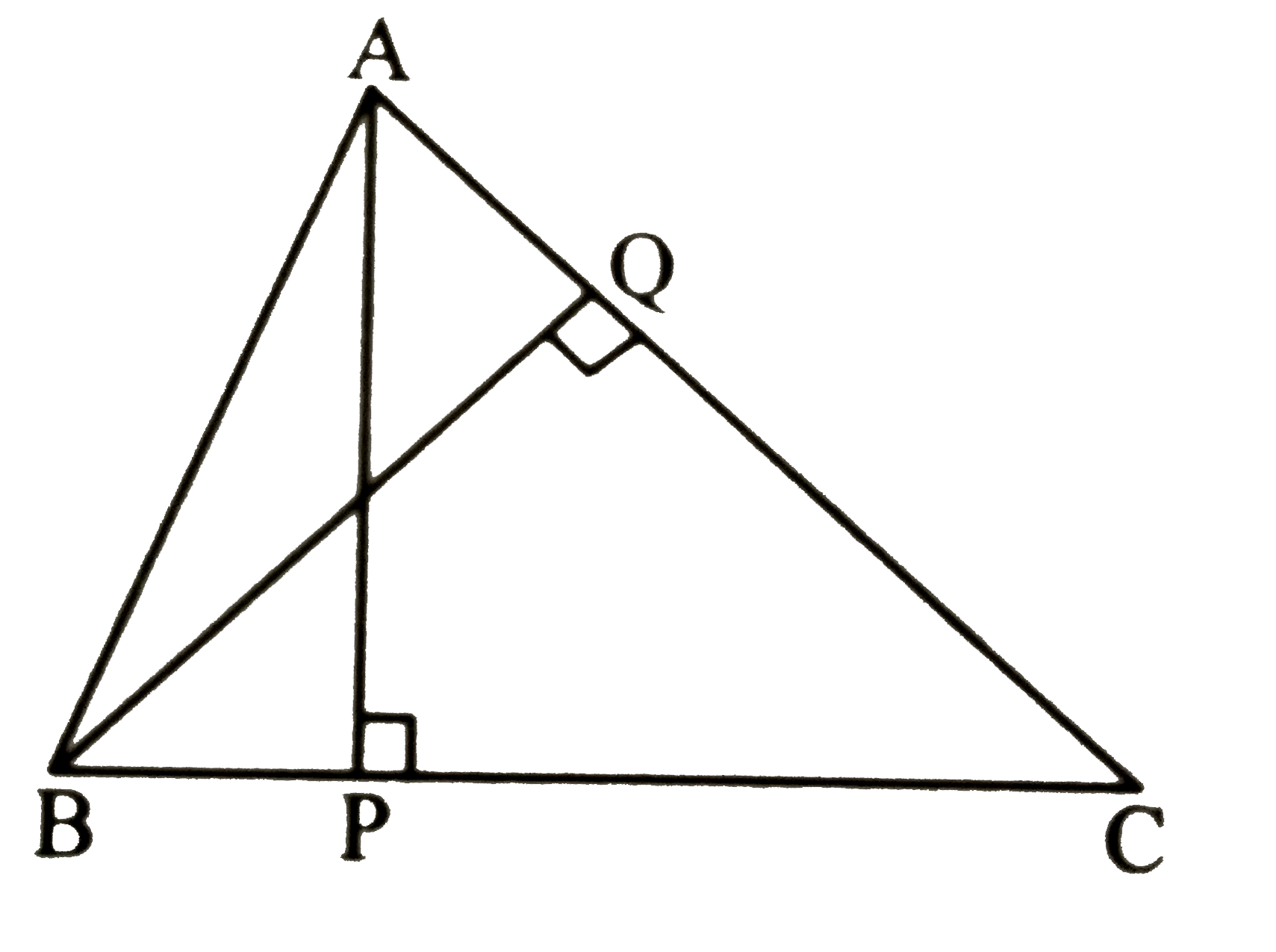
In DeltaABC, AP _|_BC, BQ_|_AC. B-P-C,A-Q-C, then prove that DeltaCPA~DeltaCQB . If AP=7, BQ=8, BC=12 then find AC.

In right-angled DeltaABC , if angle B=90^(@) , AB = 6 , BC=8, then find AC.

If a:b = 2:1 and b:c = 4:1 , then find a:c .

In DeltaABC , B - D - C and BD = 7, BC = 20 , then find the ratio (A(DeltaABD))/(A(DeltaABC))

In DeltaABC , B - D - C and BD = 7, BC = 20 , then find the ratio. (A(DeltaABD))/(A(DeltaADC))

In the figure, DeltaABC ~ DeltaAPQ . If AB 12 cm, and AQ =1/4 AC, then the length of AP is

In the adjoining figure, BC bot AB, AD bot AB, BC = 4 , AD = 8, then find (A(DeltaABC))/(A(DeltaADB)) ..

In the adjoining figure, PQ bot BC, AD bot BC, then find ratio (A(DeltaABC))/(A(DeltaADC)) .

In the adjoining figure, PQ bot BC, AD bot BC, then find ratio (A(DeltaPBC))/(A(DeltaABC)) .

In triangle ABC , seg AP is a median. If BC=18 , AB^2+AC^2=260 , then find AP.