Topper's Solved these Questions
AREAS OF PARALLELOGRAMS AND TRIANGLES
SWAN PUBLICATION|Exercise EXERCISE 9.3|21 VideosAREAS OF PARALLELOGRAMS AND TRIANGLES
SWAN PUBLICATION|Exercise EXERCISE 9.4|21 VideosAREAS OF PARALLELOGRAMS AND TRIANGLES
SWAN PUBLICATION|Exercise OBJECTIVE TYPE QUESTIONS |20 VideosCIRCLES
SWAN PUBLICATION|Exercise Objective Type Questions (Fill in the Blanks :)|10 Videos
Similar Questions
Explore conceptually related problems
SWAN PUBLICATION-AREAS OF PARALLELOGRAMS AND TRIANGLES -EXERCISE 9.2
- In Fig ., ABCD is parallologram , AEbotDCandCFbotAD . If AB= = 16...
Text Solution
|
- If E , F G and H are respectively the mid -points of the sides...
Text Solution
|
- P and Q are any two points lying on the sides DC and AD respectively o...
Text Solution
|
- In Fig ., P is a point in the interior of a parallelogram ABC...
Text Solution
|
- In Fig ., P is a point in the interior of a parallelogram ABC...
Text Solution
|
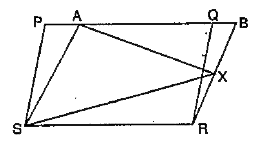
- In Fig ., PQRS and ABRS are parallelograms and X is any point o...
Text Solution
|
- In Fig ., PQRS and ABRS are parallelograms and X is any point o...
Text Solution
|
- A farmer was having a field in the form of a parallelogram PQRS. She t...
Text Solution
|