Home
Class 10
MATHS
A vertical flagstaff stands on a horizon...

A vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation the its top is 30°. Find the height of the flqgstaf.

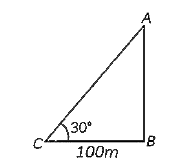
Text Solution

Verified by Experts

The correct Answer is:
`(100/sqrt3)` m.
Promotional Banner

Topper's Solved these Questions

  • INTRODUCTION TO TRIGNOMETRY AND ITS APPLICATIONS

    EDUCART PUBLICATION|Exercise SHORT ANSWER (SA-II) TYPE QUESTIONS |27 Videos

  • INTRODUCTION TO TRIGNOMETRY AND ITS APPLICATIONS

    EDUCART PUBLICATION|Exercise LONG ANSWER TYPE QUESTIONS |42 Videos

  • INTRODUCTION TO TRIGNOMETRY AND ITS APPLICATIONS

    EDUCART PUBLICATION|Exercise OBJECTIVE TYPE QUESTIONS ( VERY SHORT ANSWER TYPE QUESTIONS )|11 Videos

  • COORDINATE GEOMETRY

    EDUCART PUBLICATION|Exercise LONG ANSWER (LA) TYPE QUESTIONS (4 MARKS) |7 Videos

  • PAIR OF LINEAR EQUATIONS IN TWO VARIABLES

    EDUCART PUBLICATION|Exercise LONG ANSWER Type Questions [4 marks]|10 Videos

Similar Questions

Explore conceptually related problems

A vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation of its top is found to be 45^(@) . Find the height of the flagstaff.

A lamp post stands on a horizontal plane. From a point situated at a distance 150 m from its foot, the angle of elevation of the top is 30^(@) . What is the height of the lamp post?

A lamp post stands on a horizontal plane. From a point situated at a distance 150 m from its foot, the angle of elevation of the top is 30^(@). What is the height of the lamp post?

A 7 m long flagstaff is fixed on the top of a tower on the horizontal plane. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 45^(@)" and " 30^(@) respectively. Find the height of the tower.

From a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30^(@) . The height of the tower is

At a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30^@ The height of the tower is

The angle of elevation of the top of a vertical tower from a point on the ground is 60. From another point 10m vertically above the first, its angle of elevation is 30. Find the height of the tower.

A vertical tower stands on a horizontal plane and is surmounted by vertical flagstaff to height 6m. At a point on the plane, the anglea elevation of the bottom of flagsteff is 30^(@) and that of the top of the flagstaff is 60^(@) . Find the height of the tower. [Use sqrt(3) = 1.732 ]

Two flagstaffs stand on a horizontal plane. A and B are two points on the line joining their feet and between them. The angle of elevation of the tops of the flagstaffs as seen from A are 30^(@)and 60^(@) and as seen from B are 60^(@) and 45^(@). If AB is 30 m, the distance between the flagstaffs in metre is