Home
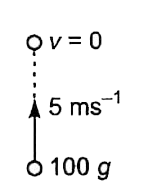
Class 12
PHYSICS
Find the work done by the force of gra...

Find the work done by the force of
gravity during the upward
journey when a particle of mass
100 g is thrown vertically upwards
with a speed of 5 `ms^(-1)`

A

`-0.5 J`

B

`-1.25 J`

C

1.25 J

D

0.5 J

Text Solution

Verified by Experts

The correct Answer is:
B
The height (h) traversed by
particle while going up is
`h=(u^(2))/(2g)=(25)/(2 xx 9.8)`

work done by gravity force=mg . H
`=0.1 xx g xx(25)/(2 xx 9.8)cos 180^(@)`
[ angle between force and
displacement is `180^(@)`]
`therefore" "W=-0.1 xx (25)/(2)=-1.25 J`
Promotional Banner

Topper's Solved these Questions

  • NTA TPC JEE MAIN TEST 30

    NTA MOCK TESTS|Exercise PHYSICS (SUBJECTIVE NUMERICAL)|10 Videos

  • NTA TPC JEE MAIN TEST 124

    NTA MOCK TESTS|Exercise PHYSICS |30 Videos

  • NTA TPC JEE MAIN TEST 36

    NTA MOCK TESTS|Exercise PHYSICS |30 Videos

Similar Questions

Explore conceptually related problems

A ball is thrown downwards with a speed of 20 ms^(–1) from top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30 ms^(–1) from the foot of the building. Find the time after which both the balls will meet - (g = 10 ms^(–2))

Find the maximum height reached by a particle which is thrown vertically upwards with the velocity of 20 m//s (take g= 10 m//s^(2) ).

Find the work done to bring 4 particle each of mass 100 gram from distances to the vertices of a square of side 20 cm .

A person in an elevator accelerating upwards with an acceleration of 4 ms^(-2) tosses a coin vertically. Upwards with a speed of 21 ms^(-1) with respect to himself. The time at which coin will back into his hand is (g = 10 ms^(-2))

A stone of mass 0.4 kg is thrown vertically up with a speed of 9.8 ms^(-1) . Find the potential energy after half second.

A particle is unchanged and is thrown vertically upward from ground level with a speed of 5sqrt(5) m//s in a region of space having uniform electric field As a result, it attains a maximum height h. The particle is then given a positive charge +q and reaches the same maximum height h when thrown vertically upward with a speed of 13 m//s Finally the particle is given a negative charge -q Ignoring air resistance determine the speed (in m//s) with which the negatively charged particle must be thrown vertically upward, so that it attains exactly the same maximum height h.

A particle when thrown obliquely from ground, can have a maximum horizontal range 'X'. When it is thrown vertically upwards with the same speed, the maximum height reached by the particle, will be 2 Х 2x √2

A ball of mass 200g is attached to a string of length 50cm and a force F is applied on it as shown. Find the work done by this force if string makes an angle 60^@ with vertical. In the initial and final position, speed of the ball is zero.

Find the work done to bring 4 particles each of mass 100 gram from large distances to the vertices of square of side 20 cm.