A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NTA MOCK TESTS-NTA TPC JEE MAIN TEST 108-PHYSICS (SUBJECTIVE NUMERICAL)
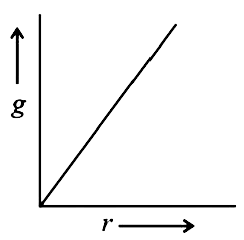
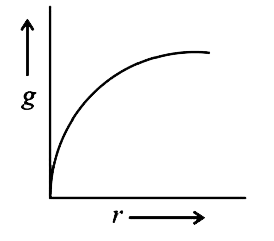
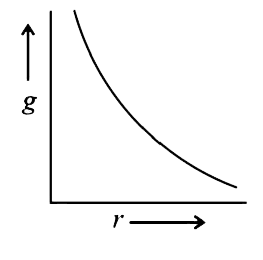
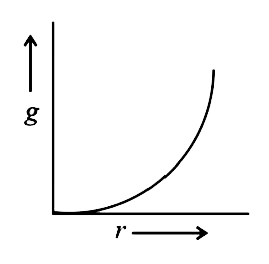
- If the density of a planet is constant, then the curve between value o...
Text Solution
|
- Find the wavelength of the K(alpha) line in copper (Z=29), if the wav...
Text Solution
|
- An electric current is passed through a circuit containing two wires o...
Text Solution
|
- In the given circuit, what is the current ( in A ) through the battery...
Text Solution
|
- What is the value of alpha? If a vector 2hati+3hatj+2hatk is perpendic...
Text Solution
|
- In the given figure magnetic field at the centre of ring O is (8)/(sqr...
Text Solution
|
- A spring of force constant 200Nm^(-1) has a block of mass 10 kg hangin...
Text Solution
|
- Consider the vernier callipers shown below. The instrument has no zero...
Text Solution
|
- Bulk modulus of metal is 10^(10)N//m^(2) and its density is 11g//cm^(3...
Text Solution
|
- A liquid having a coefficient of volume expansion gamma is filled in a...
Text Solution
|
- A man slowly pulls a bucket of water from a well of depth h=20m. The m...
Text Solution
|