Home
Class 12
MATHS
Based on the given shaded region as the ...

Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y is maximum?

A

Point B

B

Point C

C

Point D

D

every point on the line segment CD

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • CBSE TERM -1 SAMPLE PAPER 1

    EDUCART PUBLICATION|Exercise SECTION - B|20 Videos

  • CBSE TERM -1 SAMPLE PAPER 1

    EDUCART PUBLICATION|Exercise SECTION - C|4 Videos

  • SAMPLE PAPER 8

    EDUCART PUBLICATION|Exercise SECTION - C|9 Videos

  • SAMPLE PAPER (SELF-ASSESSMENT) -10

    EDUCART PUBLICATION|Exercise SECTION - C|5 Videos

Similar Questions

Explore conceptually related problems

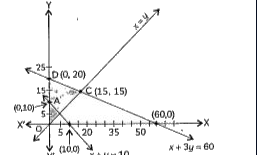
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?

The feasible region is the set of point which satisfy

In the given graph, the feasible region for a LPP is shaded. The objective function Z = 2x – 3y, will be minimum at:

In the given figure, if the shaded region is the feasible region and the objective function is z = x - 2y, the minimum value of Z occurs at:

Consider the following statements I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist . II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region. Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region. IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite. Which of the following statements are true?

The shaded part of the given figure indicates the feasible region Then the constraints are

The shaded part of the given figure indicates the feasible region Then the constraints are

In the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.

The shaded region for the inequality x+5y le 6 is

The feasible regions for two LPP is show in the following figure. Based on the given information, answer the following questions: If R_(2) is the feasible region and the objective function is Z_(2) = 4x + 3y, then the minimum value of Z_(2) occurs at: