Home
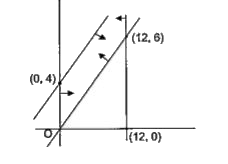
Class 12
MATHS
The feasible region for an LPP is shown ...

The feasible region for an LPP is shown in the below. Let F = 3x - 4y be the objective function. Maximum value of F is :

A

0

B

8

C

12

D

`-18`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • SAMPLE PAPER 4

    EDUCART PUBLICATION|Exercise SECTION - B|20 Videos

  • SAMPLE PAPER 4

    EDUCART PUBLICATION|Exercise SECTION - C|7 Videos

  • SAMPLE PAPER 3

    EDUCART PUBLICATION|Exercise Section - C|7 Videos

  • SAMPLE PAPER 6

    EDUCART PUBLICATION|Exercise SECTION - C |9 Videos

Similar Questions

Explore conceptually related problems

The feasible region for an LPP is shown in the following figure. Let F=3x--4y be the objective function. Maximum value of F is

The feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :

The feasible solution for a LPP is hown as below, Let Z =3x -4y be the objective function . Then, Maximum of Z occurs at

The feasible solution for a LPP is hown as below, Let Z =3x -4y be the objective function . Then, Minimum of Z occurs at

The feasible solution for a LPP is shown in following figure. Let Z=3x-4y be the objective function, Minimum of Z occurs at

The corner points of the feasible region determined by the system of linear constraints are as shown below: Let Z=3x -4y be the objective function. Find the maximum and minimum value of Z and also the corresponding points at which the maximum and minimum value occurs.

The feasible region of an LPP is shown in the figure. If z=3x+9y ,then the minimum value of z occurs at

The feasible region of a sytem of linear inequations is shown below. If Z = 2x + y, then the minimum value of Z is:

The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

Corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8) , and (0,5) . Let F = 4x+6y be the objective function. Determine the minimum value of F occurs at