Home
Class 12
MATHS
The feasible region of a sytem of linear...

The feasible region of a sytem of linear inequations is shown below. If Z = 2x + y, then the minimum value of Z is:

A

0

B

3

C

4

D

10

Text Solution

Verified by Experts

Promotional Banner

Topper's Solved these Questions

  • SAMPLE PAPER 09

    EDUCART PUBLICATION|Exercise SECTIONS-C|8 Videos

  • SAMPLE PAPER 09

    EDUCART PUBLICATION|Exercise SECTIONS-C|8 Videos

  • SAMPLE PAPER - 5

    EDUCART PUBLICATION|Exercise Section - C|10 Videos

  • SAMPLE PAPER 11

    EDUCART PUBLICATION|Exercise SECTION- C|4 Videos

Similar Questions

Explore conceptually related problems

The feasible region of a system of linear inequalities is shown below. If the objective function is maximise Z = 25x + 15y, then the maximum value of Z occurs at:

The feasible region of a system of linear inequations is shown shaded in the following figure If Z =4x +3y," then "Z_(max) - Z_(min)=

The feasible region by a system of linear inequalities is shown shaded in the given graph. If Z = 4x - 6y, then Z_("min") =

The feasible region of a system of linear inequalities is shown shaded in the following graph . If the objective function is Z = ax + by where a,b are constants and the maximum of Z occurs at points A and D then :

The feasible regions for two LPP is show in the following figure. Based on the given information, answer the following questions: If R_(2) is the feasible region and the objective function is Z_(2) = 4x + 3y, then the minimum value of Z_(2) occurs at:

A feasible region of a system of linear inequalities is said to be ..., if it can be enclosed within a circle.

The feasible region of the system of linear inequations x+2yle120,x+yge60,x-2yge0,x,yge0 :

The feasible region for an LPP is shown in the below. Let F = 3x - 4y be the objective function. Maximum value of F is :

Which of the following is a corner point of the feasible region of system of linear inequations 2x + 3y lt=6 , x + 4y lt= 4 and x, y gt= 0 ?

The feasible regions for two LPP is show in the following figure. Based on the given information, answer the following questions: If R_(1) is the feasible region, and the ojective function is Z_(1) = 2x - y , then the maximum value of Z_(1) occurs at:

EDUCART PUBLICATION-SAMPLE PAPER 09-SECTIONS-B
  1. If y=sin ^(-1) ((2^(x+1))/( 1+4^(x))),then (dy)/(dx) =

    Text Solution

    |

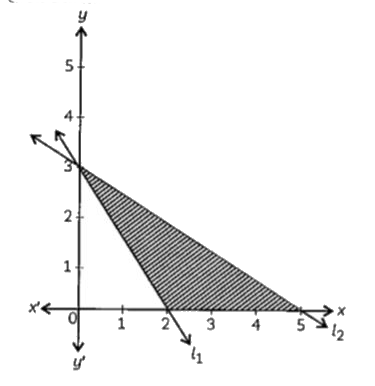
  2. The feasible region of a sytem of linear inequations is shown below. I...

    Text Solution

    |

  3. The function f(x)=x^(2)-x+1 is :

    Text Solution

    |

  4. If A^(-1)=[(0,1,-2),(-2,9,-23),(-1,5,-13)],B^(T)=[11-5-3] and X=A^(-1)...

    Text Solution

    |

  5. Let A={1,2,3,......,} and the relation R defined as (a, b) R (c,d) if ...

    Text Solution

    |

  6. The value of sin((pi)/(2)+2sin^(-1)(1)) is:

    Text Solution

    |

  7. If A is a square matrix of order n×n such that find the value of |5Aa...

    Text Solution

    |

  8. The values of a and b if the function f(x)={{:(x^(2)+3x+a",",xle1),(bx...

    Text Solution

    |

  9. If e^(v)+e^(u)=e^(v+u), then (du)/(dv)=

    Text Solution

    |

  10. The corner points of a feasible region determined by a system of linea...

    Text Solution

    |

  11. The function f:(-oo,0)to(-1,0) defined by f(x)=(x)/(1+|x|) is :

    Text Solution

    |

  12. The principal value of sec^(-1)(-(2)/(sqrt3)) is :

    Text Solution

    |

  13. If [(a+4,3b),(8,-6)]=[(2a+2,b+2),(8,a-8b)], the the respective values ...

    Text Solution

    |

  14. If A is a square matrix of order 3 such that |adjA|=64, then the value...

    Text Solution

    |

  15. Which of the following functions is decreasing on (0,(pi)/(2))?

    Text Solution

    |

  16. The local maximum value of the function f(x)=((x-1)(x-6))/(x-10) is:

    Text Solution

    |

  17. If |A|=|(a,4),(4,a)| and |A^(3)|=729, then the value of a is :

    Text Solution

    |

  18. If y=10^(10^(x)) then (dy)/(dx) is :

    Text Solution

    |

  19. Asha and Kiran went to a market to buy some stationary. Asha bought 5 ...

    Text Solution

    |