Text Solution
Verified by Experts
Topper's Solved these Questions
ELEMENTS OF VECTORS
AAKASH SERIES|Exercise LONG ANSWER TYPE QUESTIONS|5 VideosELEMENTS OF VECTORS
AAKASH SERIES|Exercise SHORT ANSWER TYPE QUESTIONS|10 VideosELECTROSTATICS
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)|5 VideosGEOMETRICAL OPTICS
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-ELEMENTS OF VECTORS-QUESTIONS FOR DESCRIPTIVE ANSWERS
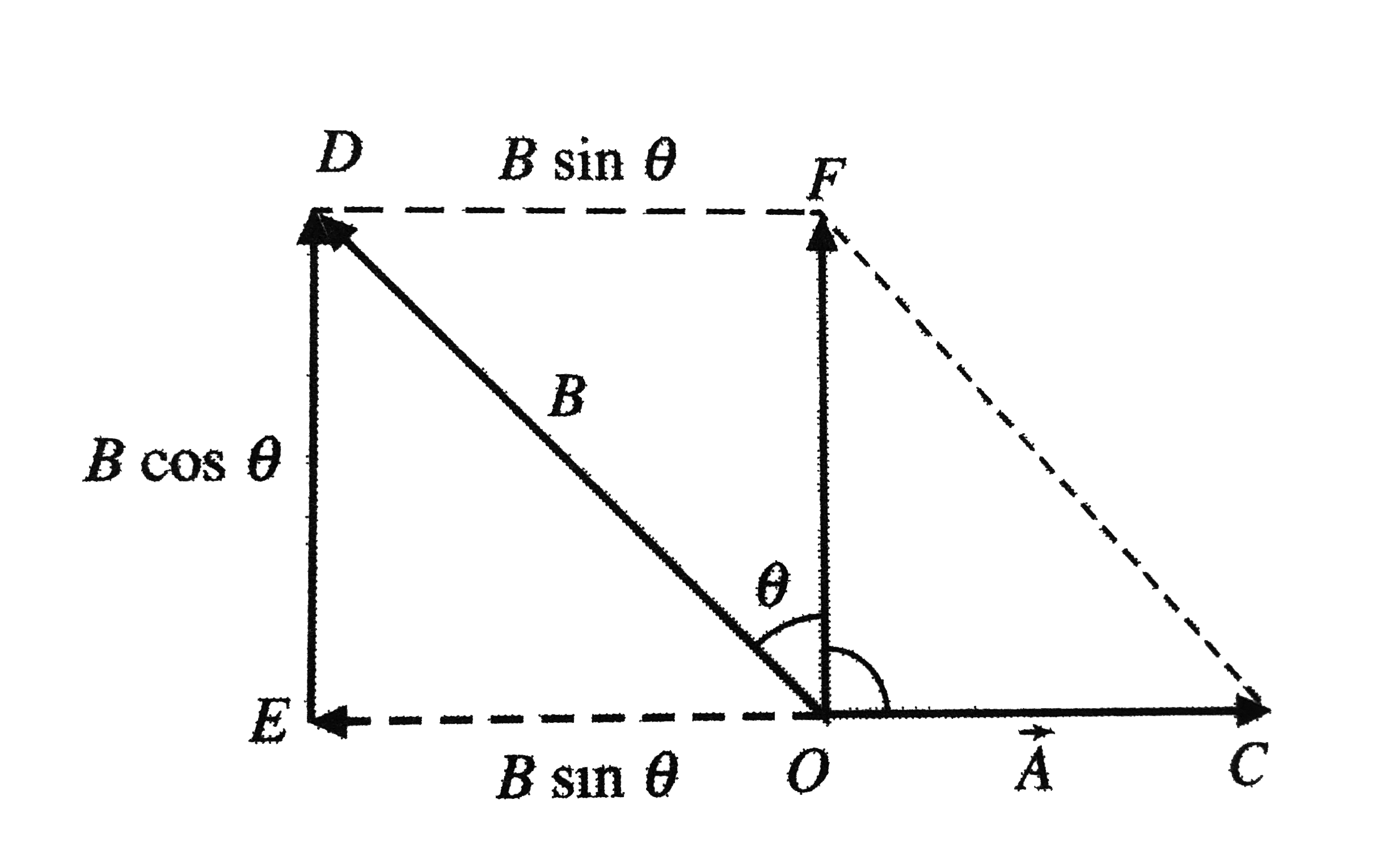
- The resultant of two vectors vecA and vecB is perpendicular to the vec...
Text Solution
|
- Find the components of a vector A = 2hati + 3hatj along the direction...
Text Solution
|
- Three vector each of magnitude A are acting at a point such that angl...
Text Solution
|
- A man can swim at the rate of 5 km h^-1 in still water. A 1 - km wide ...
Text Solution
|
- Two cars A and B are moving west to east and south to north, respectiv...
Text Solution
|
- Two ships A and B are 4 km apart. A is due west of B. If A moves with ...
Text Solution
|
- A vector barQ which has a magnitude of 8 is added to the vector barP w...
Text Solution
|
- Four vectors bara ,barb,barc, and bard are lying in the same plane. T...
Text Solution
|
- A man is travelling at 10.8 kmph in a topless car on a rainy day. He h...
Text Solution
|
- An observer is travelling in east with a velocity of 2 m/s and observe...
Text Solution
|
- The adjacent sides of a parallelogram A B C D measure 34 c ma n d20 c ...
Text Solution
|
 .
.