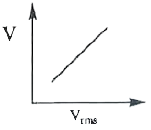
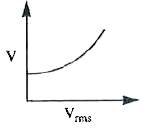
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
WAVES
AAKASH SERIES|Exercise EXERCISE-II (Pipes)|13 VideosWAVES
AAKASH SERIES|Exercise EXERCISE-II (Beats : )|20 VideosWAVES
AAKASH SERIES|Exercise EXERCISE-II (Strings (Speed of a travelling wave:))|23 VideosWAVE OPTICS
AAKASH SERIES|Exercise PROBLEMS (LEVEL - II)|33 VideosWAVES OPTICS
AAKASH SERIES|Exercise EXERCISE -III (POLARISITION)|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-WAVES-EXERCISE-II (Velocity of Sound:)
- The temperature at which the speed of sound in air becomes double of i...
Text Solution
|
- The ratio of the speed of sound in nitrogen gas to that in helium gas ...
Text Solution
|
- The speed of sound in air at 15^(@)C and 76 cm of Hg is 340 m/s. The s...
Text Solution
|
- The velocities of sound in an ideal gas at temperature T(1) and T(2) K...
Text Solution
|
- v(1) and v(2) are the velocities of sound at the same temperature in t...
Text Solution
|
- For an ideal gas, the graph representing the variation of the speed of...
Text Solution
|
- The speed of sound in oxygen (O(2)) at a certain temperature is 460 ms...
Text Solution
|
- A steel rod 100 cm long is dampled at into middle.Then fundamental fre...
Text Solution
|