Home
Class 11
PHYSICS
A disc of mass 500 g and radius 10 cm ca...

A disc of mass 500 g and radius 10 cm can freely rotate about a fixed axis as shown in figure. light and inextensible string is wound several turns around it and 100 g body is suspended at its free end. Find the acceleration of this mass. [Given: The string makes the disc to rotate and does not slip over it. g = 10 m `s^(-2)`.

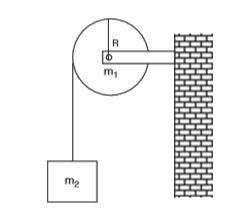
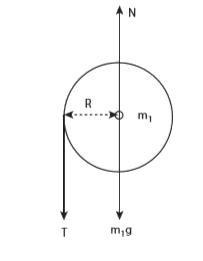
Text Solution

Verified by Experts


Let the mass of the disc be `m_(1)` and its radius R. The mass of the suspended body is `m_(2)`.
`m_(1)` = 500 g = `500×10^(−3)` kg =0.5 kg
`m_(2)` = 100 g = `100×10^(−3)` kg = 0.1 kg
As the light inextensible string is wound around the disc several times it makes the disc rotate without slipping over it. The translational acceleration of m2 and tangential acceleration of m1 will be the same. Let us draw the free body diagram (FBD) of `m_(1)` and `m_(2)` separately.
Promotional Banner

Topper's Solved these Questions

  • MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES

    NCERT TAMIL|Exercise EXERCISE (I. MULTI CHOICE QUESTION) |15 Videos

  • MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES

    NCERT TAMIL|Exercise EXERCISE (V. NUMERICAL PROBLEMS) |6 Videos

  • MOTION IN A STRAIGHT LINE

    NCERT TAMIL|Exercise ADDITIONAL EXERCISES|5 Videos

  • NATURE OF PHYSICAL WORLD AND MEASUREMENT

    NCERT TAMIL|Exercise EXERCISE (V. Conceptual Questions)|5 Videos

Similar Questions

Explore conceptually related problems

A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

A constant force F=m_2g/s is applied on the block of mass m_1 as shown in figure. The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m_1

A wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rad s^-2 in the wheel. Calculate the moment of inertia of the wheel.

A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleratrion of 2 revolutions s^-2 is

The pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.

The pulley shown in figure has a moment of inertias I about its axis and mass m. find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

A uniform circular disc of mass 200 g and radius 4.0 cm is rotated about one of its diameter at an angular speed of 10 rad/s. Find the kinetic energy of the disc and its angular momentum about the axis of rotation.

Calculate the tension in the string shown in figure. The pulley and the string are light and all surfaces are frictionless. Take g=10 m/ s^2 .

A body of mass 5kg is suspended by a spring balance on an inclined plane as shown in the figure. the spring balance measures [g=10 m/s^(2)]

A wheel of moment of inertia 0.500 kg-m^2 and radius 20.0 cm is rotating about its axis at an angular speed of 20.0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.