Home
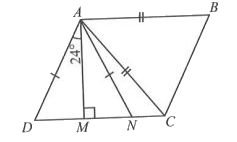
Class 8
MATHS
If ABCD is a parallelogram, Delta ADN an...

If ABCD is a parallelogram, `Delta ADN and Delta ABC` are isosceles triangles, then find `angleBAC`.

A

`112^(@)`

B

`140^(@)`

C

`48^(@)`

D

`32^(@)`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • IMO QUESTION PAPER 2018-19 SET- A

    SCIENCE OLYMPIAD FOUNDATION |Exercise Everyday Mathematics|10 Videos

  • IMO QUESTION PAPER 2018-19 SET- A

    SCIENCE OLYMPIAD FOUNDATION |Exercise Achievers Section|5 Videos

  • IMO QUESTION PAPER 2018-19 SET -B

    SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION|5 Videos

  • IMO QUESTION PAPER 2019-20 SET A

    SCIENCE OLYMPIAD FOUNDATION |Exercise Achievers Section|5 Videos

Similar Questions

Explore conceptually related problems

If ABCD is a parallelogram DeltaADN and DeltaABC are isosceles triangles, then find /_BAC .

In figure ABC is an isosceles triangle , right angled at C . Therefore

The area of a parallelogram ABCD is equal to that right angled isosceles triangle whose hypotenuse is l cm. If O is a point inside the parallelogram ABCD then sum of areas of DeltaAOBandDeltaCOD is.

In the given figure (not to scale), ABC is an isosceles triangle in which AB=AC. AEDC is a parallelogram. If angleCDF=70^(@) and angleBFE=180^(@) , then find angleFBA .

In the given figure, ABCD is a parallelogram. Find the area of Delta AED

In the adjoining figure, Delta ABC is an isosceles triangle. Find the value of angleBDC and angleBEC .

In an isosceles triangle ABC, AB=AC and angleA=3angleB. Find angleC .

In the adjoning figure, ABCD is a parallelogram. Prove that : area of Delta BPC = " area of " Delta DPQ

In the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that angle DAC = angleDCA. Consider the following statements : 1. Triangle ADC is an isosceles triangle. 2. Dis the centroid of the triangle ABC. 3. Triangle ABD is congruent to the triangle CBD. Which of the above statements are correct ?