A
B
C
D
लिखित उत्तर
Verified by Experts
The correct Answer is:
टॉपर्स ने हल किए ये सवाल
JEE ADVANCED पेपर - 2 (2021)
JEE Main & Advanced (Hindi Medium)|Exercise MATHEMATICS (खंड-2)|6 VideosJEE ADVANCED पेपर - 2 (2021)
JEE Main & Advanced (Hindi Medium)|Exercise MATHEMATICS (खंड-3)|4 VideosJEE ADVANCED पेपर - 2 (2016)
JEE Main & Advanced (Hindi Medium)|Exercise भाग- III गणित (खंड-3)|4 VideosJEE ADVANCED सॉल्वड पेपर 2019
JEE Main & Advanced (Hindi Medium)|Exercise पेपर 2 खण्ड 3|4 Videos
JEE Main & Advanced (Hindi Medium)-JEE ADVANCED पेपर - 2 (2021)-MATHEMATICS (खंड-4)
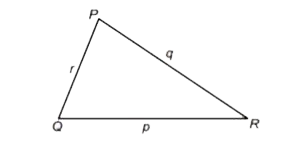
- एक त्रिभुज PQR पर विचार कीजिए जिसके कोण P,Q, R की सम्मुख भुजाओं की लम्...
Text Solution
|
- समुच्चय {1, 2, 3......, 2000} में से एक संख्या का यादृच्छया चयन किया ज...
Text Solution
|
- माना E, दीर्घवृत्त x^2/16 +y^2/9=1 है। E पर किन्हीं तीन भिन्न बिंदुओं ...
Text Solution
|
- किसी वास्तविक संख्या x के लिए, माना [x], x के बराबर या इससे कम महत्तम ...
Text Solution
|