किसी वास्तविक संख्या x के लिए, माना [x], x के बराबर या इससे कम महत्तम पूर्णांक को निरूपित करता है। यदि `I=int_(0)^(10)[sqrt((10x)/(x+1))]dx` तब 9I का मान _____ है

Answer

`182.00`

Explanation

`I=int_0^(10)[sqrt((10x)/(x+1))]dx`
` y = (10x)/(x+1) , 0 le x le10`
`xy + y = 10x`
`x=y/(10-y)`
`0 le y/(10-y) le10`
`y/(10-y) ge0` तथा `y/(10 -y) -10 le 0`
` y/(10-y) le0` तथा `(11y -100)/(y-10) ge0`

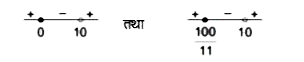
`y in [0,10)` तथा `y in (-oo, 100/11] cup (10 ,oo) `
`y in[0,100/11]`
`sqrty in[0,10/sqrt11] implies [sqrty]={0,1,2,3}`
स्थिति I : `0 le (10x)/(x+1) lt1`
`(10x)/(x+1) ge0` तथा `(10x)/(x+1)-1 lt 0`

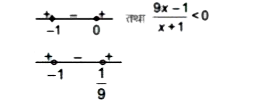
`x in(-oo,-1)cup[0,oo)` तथा `x in (-1,1/9)`
`x in [0,1/9)` तब `[sqrt((10x)/(x+1))]=0`
स्थिति II : `4 le (10x)/(x+1)lt9`
`(10x)/(x+1) -4 ge0` तथा `(10x)/(x+1)lt9`
`(6x-4)/(x+1)gt0` तथा `(10x)/(x+1) lt9`

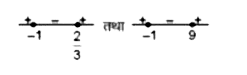
`x in (-oo,-1) cup[2/3,oo), x in(-1,9)`
`x in[2/3,9), [sqrt((10x)/(x+1))]=2`
स्थिति IV : `x in [9,10] implies [sqrt((10x)/(x+1))]=3`
`I=int_0^(1/9)0.dx+int_(1/9)^(2/3)1.dx+int_(2/3)^(9) 2.dx+int_(9)^(10)3.dx`
`I=(2/3-1/9)+2(9-2/3)+3(10-9)`
`I = 5/9 + 50/3 + 3`
9I = 182