A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ROTATIONAL MOTION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Angular Momentum)|52 VideosROTATIONAL MOTION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Work, Energy and Power)|44 VideosROTATIONAL MOTION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)|34 VideosNEWTON'S LAWS OF MOTION
ERRORLESS|Exercise ASSERTION & REASON |18 VideosSIMPLE HARMONIC MOTION
ERRORLESS|Exercise Assertion & Reason|15 Videos
Similar Questions
Explore conceptually related problems
ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Moment of Inertia)
- A string is wound round the rim of a mounted flywheel of mass 20 kg an...
Text Solution
|
- The instantaneous angular position of a point on a rotating wheel is g...
Text Solution
|
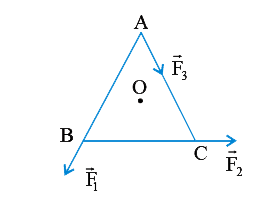
- ABC is an equilateral with O as its centre vecF(1), vecF(2) and vecF(3...
Text Solution
|
- The total torque about pivot A provided by the forces shown in the fig...
Text Solution
|
- A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate abou...
Text Solution
|
- An autmobile moves on road with a speed of 54 km//h. The radius of its...
Text Solution
|
- A rod of weight w is supported by two parallel knife edges A and B and...
Text Solution
|
- A solid sphere of mass m rolls without slipping on an inclined plain o...
Text Solution
|
- A wheel of radius R with an axle of radius R/2 is shown in the figure ...
Text Solution
|
- Consider two masses with m(1) gt m(2) connected by a light inextensibl...
Text Solution
|
- The torque of force vec(F)=-3hat(i)+hat(j)+5hat(k) acting at the point...
Text Solution
|
- Two masses m1 = 1 kg and m2 = 2 kg are connected by a light inextensib...
Text Solution
|
- A pulley fixed to the ceiling carries a string with blocks of mass m a...
Text Solution
|
- Five particles of mass 2 kg each are attached to the rim of a circular...
Text Solution
|
- The moment of inertia of a body does not depend on
Text Solution
|
- Four small objects each of mass m are fixed at the corners of a rectan...
Text Solution
|
- Three particles, each of mass m grams situated at the vertices of an e...
Text Solution
|
- Point masses 1, 2, 3 "and" 4 "kg are lying at the point (0, 0, 0), (2,...
Text Solution
|
- Four point masses, each of value m, are placed at the corners of a squ...
Text Solution
|
- A sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The m...
Text Solution
|