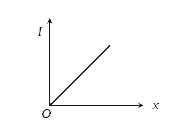
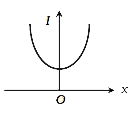
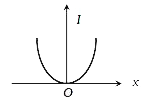
According to the theorem of parallel axe...

According to the theorem of parallel axes `I = I_("cm") + Mx^(2)`, the graph between I and x will be

Text Solution

Verified by Experts

The correct Answer is:

`I=I_(CM)+Mx^(2)`
Parabola with intercept `(I_(CM))` .

Topper's Solved these Questions

ROTATIONAL MOTION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Angular Momentum)|52 Videos
ROTATIONAL MOTION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Work, Energy and Power)|44 Videos
ROTATIONAL MOTION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)|34 Videos
NEWTON'S LAWS OF MOTION
ERRORLESS|Exercise ASSERTION & REASON |18 Videos
SIMPLE HARMONIC MOTION
ERRORLESS|Exercise Assertion & Reason|15 Videos

Similar Questions

Explore conceptually related problems

By the theorem of parallel axes:

State and prove theorem of parallel axes.

Theorem of parallel axes is applicable for

(a) Prove the theorem of perpendicular axes. (Hint : Square of the distance of a point (x, y) in the x-y plane from an axis through the origin and perpendicular to the plane is ^(x2)+y^(2)) . (b) Prove the theorem of parallel axes. (Hint : If the centre of mass of a system of n particles is chosen to be the origin summ_(i)r_(i)=0 ).

Statement-1: if moment of inertia of a rigid body is equal about two axis, then both the axis must be parallel. Statement-2 from parallel axis theorem I=I_(cm)+md^(2) , where all terms have usual meaning.

A, B and C are parallel conductors of equal length carrying currents I, I and 2I respectively. Distance between A and B is x . Distance between B and C is also x . F_(1) is the force exerted by B on A and F_(2) is the force exerted by B on A choose the correct answer

An alternating current I in an inductance coil varies with time t according to the graph as shown: Which one of the following graph gives the variation of voltage with time?

Assertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum Reason: From theorem of parallel axis I=I_(cm)+Mr^(2)

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Moment of Inertia)

In a rectangle ABCD (BC = 2 AB). The moment of inertia along which axe...
Text Solution
|
From a circular ring of mass M and radius R, an arc corresponding to a...
Text Solution
|
Find the ratio of the radii of gyration of a circular disc and a circu...
Text Solution
|
The radius of gyration of a solid shapere of radius r about a certain ...
Text Solution
|
For the given uniform square lamina ABCD, whose centre is O
Text Solution
|
From a circular disc of radius R and 9M , a small disc of mass...
Text Solution
|
The moment of inertia of a uniform rod about a perpendicular axis pass...
Text Solution
|
Three idential spherical shells each of mass m and radius r are placed...
Text Solution
|
Four spheres of diameter 2a and mass M are placed with their centres o...
Text Solution
|
A circular disc of radius R and thickness R//6 has moment of inertia I...
Text Solution
|
Two discs of same thickness but of different radii are made of two dif...
Text Solution
|
Let I be the moment of interia of a uniform square plate about an axis...
Text Solution
|
From a disc of radius R, a concentric circular portion of radius r is...
Text Solution
|
A solid cylinder has mass M radius R and length / its moment of inert...
Text Solution
|
The moment of inertia of a solid disc made of thin metal of radius R a...
Text Solution
|
Seven identical coins are rigidly arranged on a flat table in the patt...
Text Solution
|
The moments of inertia of a non-uniform circular disc (of mass M and r...
Text Solution
|
Moment of inertia of a sphere of mass M and radius R is I. Keeping M ...
Text Solution
|
According to the theorem of parallel axes I = I("cm") + Mx^(2), the g...
Text Solution
|
Point masses m(1) and m(2) are placed at the opposite ends of a rigid ...
Text Solution
|