Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-QUESTION PAPER 2022 TERM 2 SET 1-SECTION C
- Find the equations of the planes passing through the line of intersect...
Text Solution
|
- Find the particular solution of the differential equation x(dy)/(dx)+y...
Text Solution
|
- Find the general solution of the differential equation x(y^(3)+x^(3)) ...
Text Solution
|
- Evaluate : int(0)^(pi/2)(2logcosx-logsin2x)dx
Text Solution
|
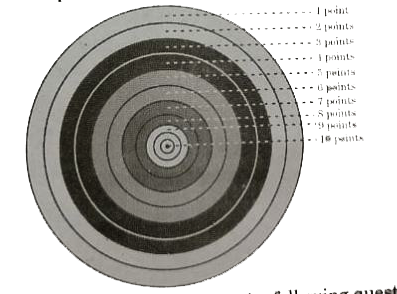
- In a game of Archery, each ring of the Archery target is valued. The c...
Text Solution
|
- In a game of Archery, each ring of the Archery target is valued. The c...
Text Solution
|