Text Solution
Verified by Experts
Topper's Solved these Questions
MECHANICAL PROPERTIES OF SOLIDS
AAKASH INSTITUTE|Exercise Try Yourself|32 VideosMECHANICAL PROPERTIES OF SOLIDS
AAKASH INSTITUTE|Exercise Assignment (SECTION - A)|31 VideosMECHANICAL PROPERTIES OF FLUIDS
AAKASH INSTITUTE|Exercise SECTION - J|9 VideosMock test 03
AAKASH INSTITUTE|Exercise EXAMPLE|37 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-MECHANICAL PROPERTIES OF SOLIDS-Assignment(Section-D)
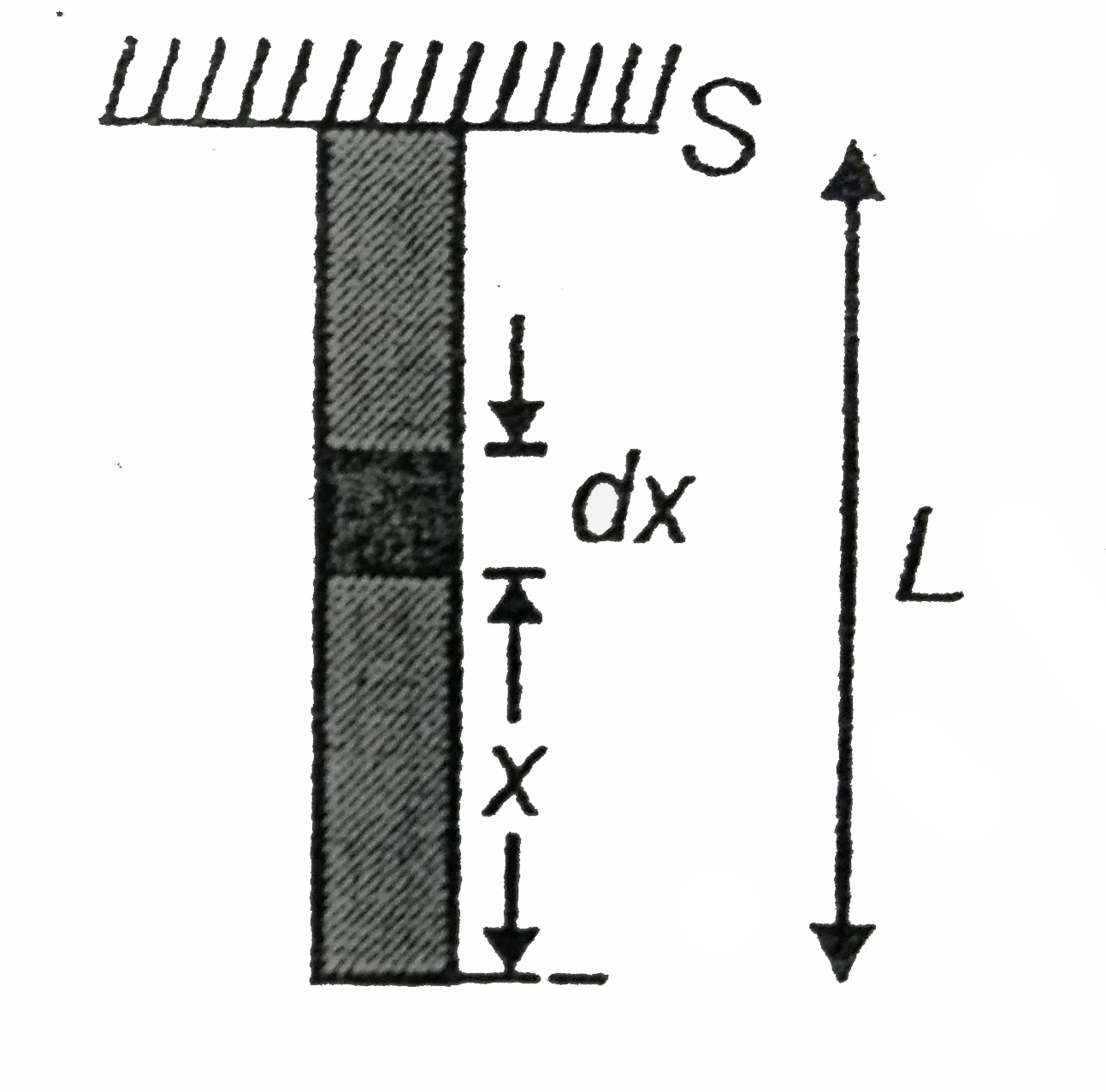
- A bar of mass M and length L is hanging from point S as shown in figur...
Text Solution
|
- According to Hooke's law of elasticity, if stress is increaed, the rat...
Text Solution
|
- A: Strain is a dimensionless quantity, R: Strain is internal force pe...
Text Solution
|
- A: Diamond is more elastic than rubber. R: When same deforming force ...
Text Solution
|
- Statement-1: Young's modulus for a perfectly plastic body is zero St...
Text Solution
|
- Statement-1: The bridges are declared unsafe after a long use. Stat...
Text Solution
|
- Assertion : Spring balances show correct readings even after they ha...
Text Solution
|
- Assertion Modulus of elasticity does not depend upon the dimensions of...
Text Solution
|
- The adiabatic elasticity of a gas is equal to
Text Solution
|
- A rectangular beam of metal supported at its two ends is loaded at the...
Text Solution
|
- A:Iron is more elastic than copper R:Under a given deforming force Iro...
Text Solution
|
- A: Lateral strain is directly proportional to the longitudinal strain ...
Text Solution
|
- Two identical springs of copper and steel are equally strectched. On w...
Text Solution
|