Home
Class 12
PHYSICS
The inclined surface is rough mu = (1)/(...

The inclined surface is rough `mu = (1)/(2)`. For different values of m and M system slides down or up the plane or remains stationary. Match the appropriate entries of column-1 with those of column-2

`{:(,"Column-1",,"Column-2"),("(A)","Minimum value of " (m)/(M) "so theta m slides down","(P)",(5)/(3)),("(B)","Minimum valie of " (M)/(m)"so that m slides up","(Q)",1),("(C)","Value of" (m)/(M) "so that friction force on m is zero","(R)",(3)/(5)),("(D)",underset("and acceleration of M")"Ratio of vertical component of acceleration of m","(S)",5):}`

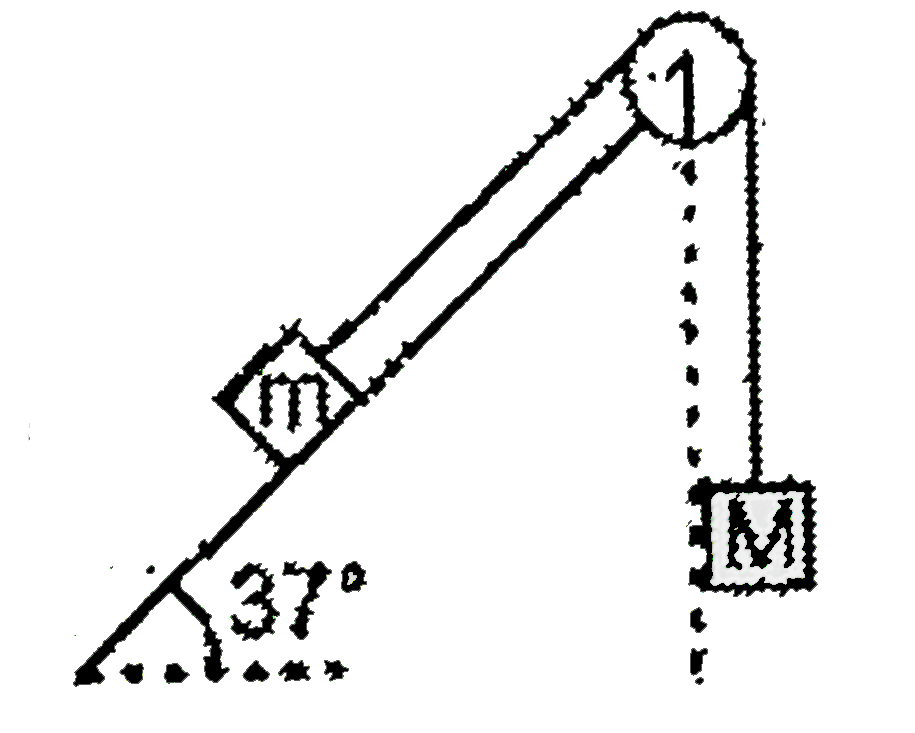
Text Solution

Verified by Experts

The correct Answer is:
A(q, r, s), B(q, r), C(p, t), D(p)
Promotional Banner

Topper's Solved these Questions

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH INSTITUTE|Exercise Assignment (SECTION - G)|2 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH INSTITUTE|Exercise Assignment (SECTION - H)|2 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    AAKASH INSTITUTE|Exercise Assignment (SECTION - E)|2 Videos

  • MECHANICAL PROPERTIES OF FLUIDS

    AAKASH INSTITUTE|Exercise SECTION - J|9 Videos

  • Mock test 03

    AAKASH INSTITUTE|Exercise EXAMPLE|37 Videos

Similar Questions

Explore conceptually related problems

Two blocks of mass 2m and m slide down the slope AB having same friction coefficient Then:

A block of mas m begins to slide down on an inclined plane of inclination theta . The force of friction will be

A body of mass m slides down a rough plane of inclination alpha . If mu is the coefficient of friction, then acceleration of the body will be

A body of mass m slides down a rough plane of inclination alpha . If mu is the coefficient of friction, then acceleration of the body will be

Match the corresponding entries of column 1 with column 2. [where m is the magnification produced by the mirror

A body weighing 20 kg just slides down a rough inclined plane that rises 5 m in every 13 m. What is the coefficient of friction?

Trajectory of a particle in a projectile motion is given by y=x-x^(2)/80 where x and y are in meters. Match the column-1 and column-2. {:(,"Column-I",,"Column-II"),("(A)","x coordinate at height of 15 m",,"(P) 20 m"),("(B)",underset("point of projection at x= 100 m")"vertical distnce of particle from",,"(Q) 80 m"),("(C)","Horizontal range",,"(R) 60 m"),(,,,"(S) 25 m"):}

The coefficent of friction between the masses 2m and m is 0.5. All other surfaces are frictionless and pulleys are massless. Column I given the different values of m_(1) and column II gives the possible acceleration of 2m and m. Match the following : {:(,"Column I",,"Column II",),((A),m_(1) = 2m,(P),"Accelerations of 2m and m are same",),((B),m_(1) = 3m,(Q),"Acceleration of 2m and m are different",),((C ),m_(1) = 4m,(R ),"Acceleration of 2m is greater than m",),((D),m_(1) = 6m,(S),"Acceleration of 2m is less than 0.6 g",),(,,(T),"Acceleration of 2m is greater than 0.6 g",):}