Home
Class 12
MATHS
The number of different circles passing ...

The number of different circles passing through the points A,B,C,D,E,F and G as shown in the adjacent figure.

Text Solution

Verified by Experts

We know that from three non-collinear points one and only one circle can be drawn.
Hence, the number of different circles.
=Number of 3 non-collinear points selected from the given figure
`=""^(5)C_(2)xx""^(2)C_(1)+""^(4)C_(1)xx""^(2)C_(2)`
`=20+4=24`
Promotional Banner

Topper's Solved these Questions

  • PERMUTATIONS AND COMBINATIONS

    AAKASH INSTITUTE|Exercise Try Yourself|65 Videos

  • PERMUTATIONS AND COMBINATIONS

    AAKASH INSTITUTE|Exercise Assignment Section A Objective type questions (One option is correct )|51 Videos

  • MATRICES

    AAKASH INSTITUTE|Exercise Assignment (Section - J) Aakash Challengers Questions|3 Videos

  • PRINCIPLE OF MATHEMATICAL

    AAKASH INSTITUTE|Exercise Section-D:(Assertion-Reason Type Questions)|12 Videos

Similar Questions

Explore conceptually related problems

The number of different triangles formed by joining the points A,B,C,D,E,F and G as shown in the figure given below is

A circle passes through A,B,C and D as shown in the figure.If /_BAD=63, find x.

Write down the co-ordinates of each points A,B,C,D,E and F as shown in following figure.

Which of the followig hormones passes through "route-A" shown in the adjacent figure?

Identify A, B, C, D, E, F,G

A network of nine conductors connects six points A,B , C,D,E and F as shown in figure -3.97. The figure denotes resistances in ohms. Find the equivalents resistance between A and D. [1 Omega]

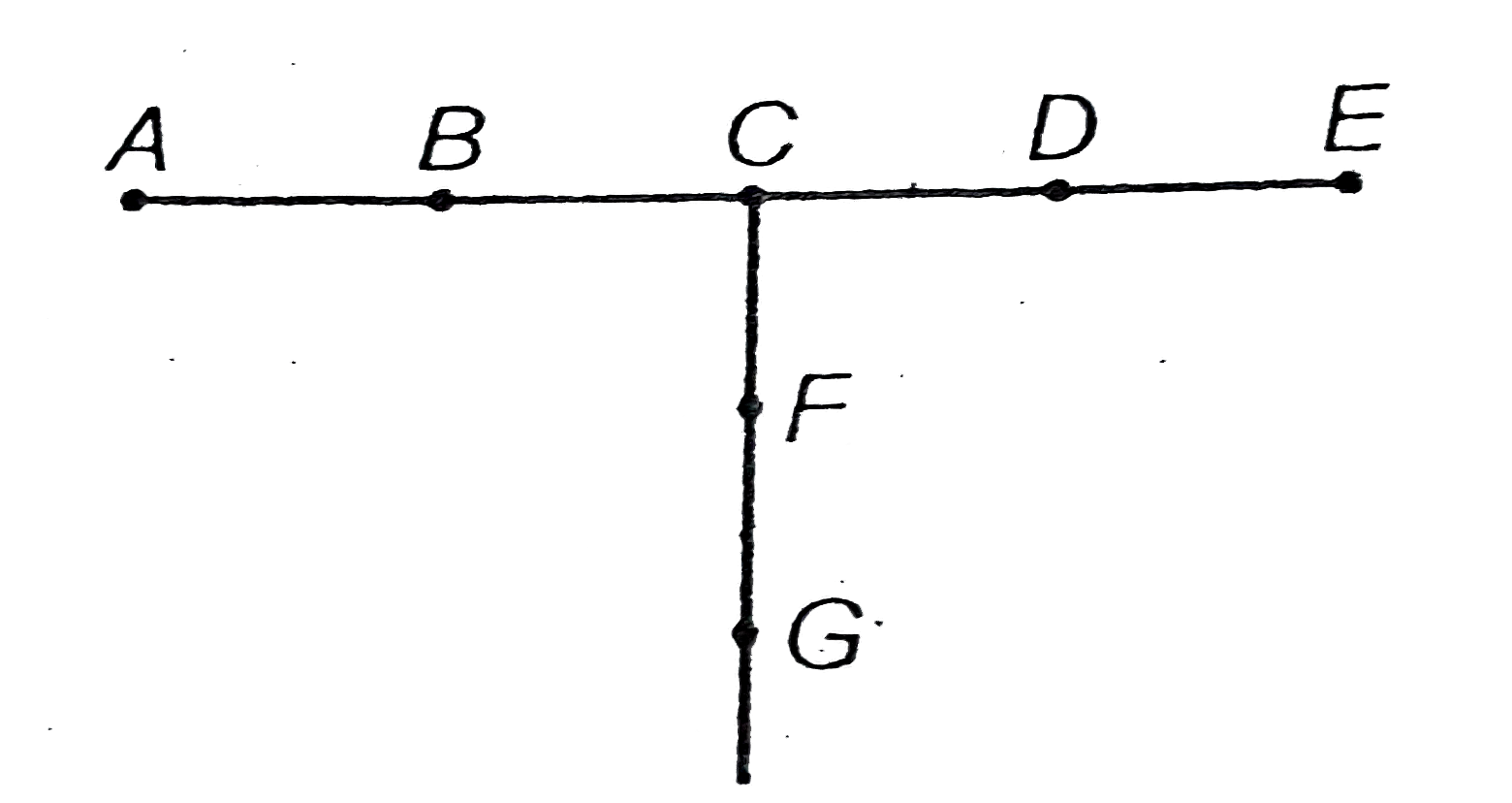
There are 10 points in a plane of which no three points are collinear and four points are concyclic.The number of different circles are can be drawn through at least three points of these points is (A) 116 (B) 120 (C) 117 (D) none of these

In the above figure,the circles with centres P,Q and R intersect at point B,C,D and E as shown. Lines CB and ED intersect in point M. Lines drawn from point M touch the circles at points A and F. Prove that MA = MF.

There are five points A,B,C,D and E. no three points are collinear and no four are concyclic. If the line AB intersects of the circles drawn through the five points. The number of points of intersection on the line apart from A and B is

In Figure,ABCD is a cyclic quadrilateral.A circle passing through A and B meets AD and BC in the points E and F respectively.Prove that EFDC