Home
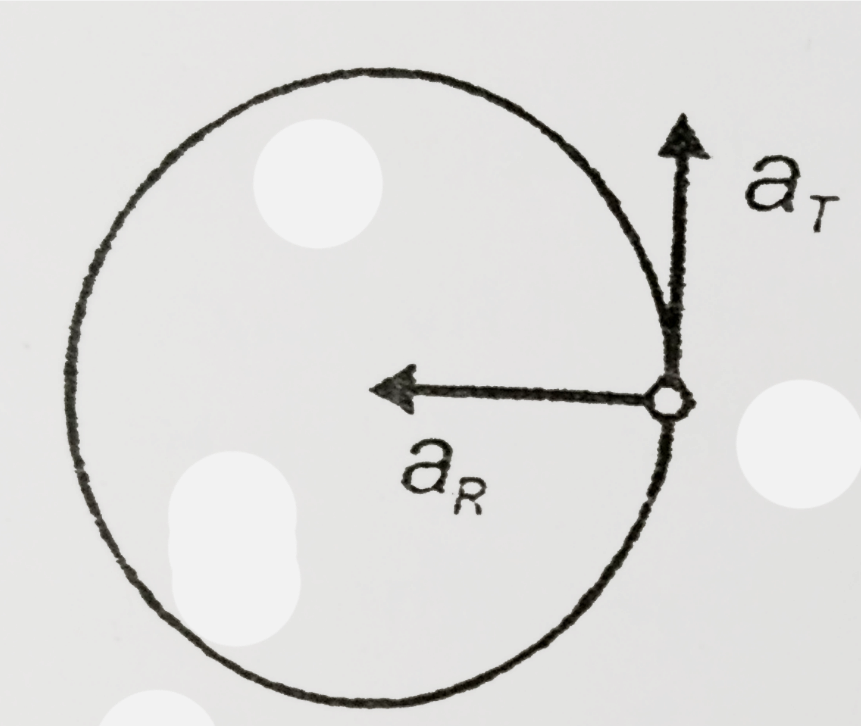
Class 12
PHYSICS
A particle moves with decreasing speed a...

A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.

The magnitude of tangential acceleration at ` t = R/(2u)` is

A

`u^(2)/R`

B

`(2u^(2))/(3R)`

C

`(4u^(2))/(9R)`

D

`(7u^(2))/(36R)`

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PLANE

    AAKASH INSTITUTE|Exercise Assignement section -E (Assertion-Reason)|3 Videos

  • MOTION IN A PLANE

    AAKASH INSTITUTE|Exercise Assignement section -G (Integer)|3 Videos

  • MOTION IN A PLANE

    AAKASH INSTITUTE|Exercise Assignement section -C Objective (More than one option is correct)|5 Videos

  • MOCK_TEST_17

    AAKASH INSTITUTE|Exercise Example|15 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 Videos

Similar Questions

Explore conceptually related problems

A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u. The time after which the speed of particle reduces to half of its initial value is

A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals v_(0) , then th speed of the particle as a function of the distance covered S will be

A particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_(0) . Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v .

A point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_0 . Find: (a) the velocity of the point as a function of time and as a function of the distance covered s_1 , (b) the total acceleration of the point as a function of velocity and the distance covered.

A particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v_(0) at t=0 , the time for the completion of the half of the first revolution will be

A particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is

A particle is performing a U.C .M along a circular path of radius r, with a uniform speed v. Its tangential and radial acceleration are

A particle starts moving with a constant angular acceleration in a circular path. The time at which the magnitudes of tangential and radial acceleration are equal is