Show how would you join three resistors, each of resistance `9 Omega` so that the equivalent resistance of the combination is (i) `13.5 Omega` , (ii) `6 Omega` ?

Explanation

(i)
Resultant resistance of `R_(1)` and `R_(2)` is R'
`1/(R' ) = (1)/(R_(1)) + (1)/(R_(2))`
`rArr (1)/(R ') = 1/9 + 1/9 = (1+1)/(9) = 2/9`
`:. R ' = 9/2 = 4.5 Omega`
Resultant resistance of R' and `R_(3)` is R
`R = R' + R_(3)`
`= 4.5 + 9 = 13.5Omega`
(ii)
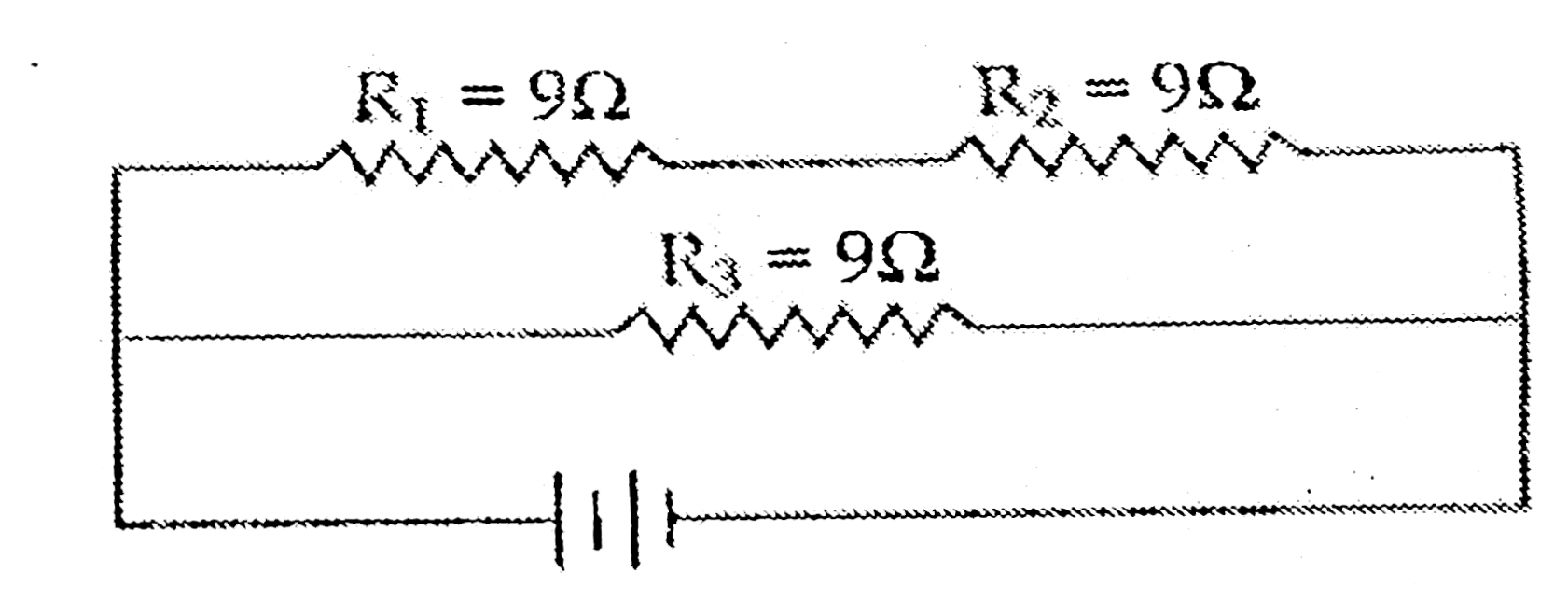
Resultant resistance of `R_(1)` and `R_(2)` is given by R'
Resultant resistance of R' and `R_(3)` is given by R
`1/R= 1/(R') = (1)/(R_(3)) = 1/18 + 1/9 = (1+2)/(18) = 3 /18 = 1/6
`R = 6 Omega`