लिखित उत्तर
Verified by Experts
BALAJI PUBLICATION-गतिमान आवेश और चुंबकत्व -NCERT पाठय-पुस्तक के हल
- एक वर्गाकार कुंडली जिसकी प्रत्येक भुजा 10 सेमी० हैं, में 20 फेरे हैं, ...
Text Solution
|
- दो चल कुंडली गालवनोमीटर मीटरों, M(1) एवं M(2) के वितरण नीचे दिए गए हैं...
Text Solution
|
- एक प्रकोष्ट में 6.5 G(1G =10^(-4)T) का एकसमान चुंबकीय क्षेत्र बनाये रख...
Text Solution
|
- वृत्तकार कक्षा में इलेक्ट्रान की परिक्रमण आवृत्ति प्राप्त कीजिये। क्या...
Text Solution
|
- (a) 30 फेरों वाली एक वृत्ताकार कुंडली जिसकी त्रिज्या 8.0 सेमी0 हैं ओर ...
Text Solution
|
- दो संकेन्द्रिक वृत्ताकार कुण्डलियाँ X ओर Y जिनकी उध्र्वाधर क्रमश: 16 स...
Text Solution
|
- 10 सेमी लम्बाई ओर 10^(-3) मीटर अनुप्रस्थ काट के एक क्षेत्र में 100 G (...
Text Solution
|
- I धारावाही, N फेरों ओर R त्रिज्या वाली वृत्ताकार कुण्डली के लिए, इसके ...
Text Solution
|
- एक टोरॉइड के (अलौह चुंबकीय) क्रोड की आतंरिक त्रिज्या 25 सेमी और बाह्म ...
Text Solution
|
- निम्नलिखित प्रशनों के उत्तर दीजिये- (a) किसी प्रकोष्ट में एक ऐसा चुं...
Text Solution
|
- उष्मत कैथोड से उत्सर्जित और 2.0 kV के विभवांतर पर त्वरित एक इलेक्ट्रान...
Text Solution
|
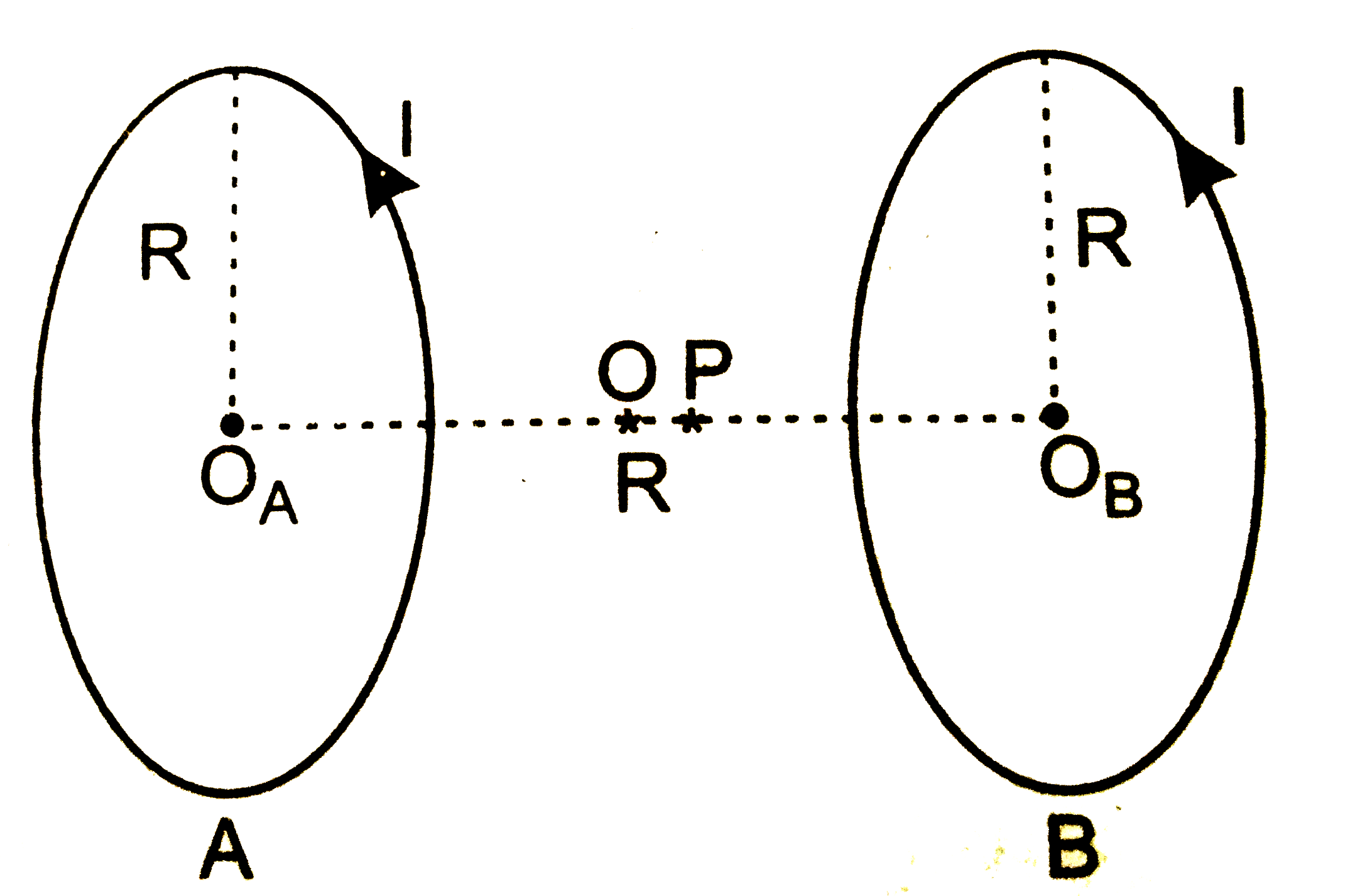
- प्रशन में वर्णित हेल्महोल्टज कुंडलियां का उपयोग करके किसी लघुशेत्र में...
Text Solution
|
- एक सीधी, क्षैतिज चालक चढ़ जिसकी लम्बाई 0.45 मीटर एवं द्रव्यमान 60 ग्राम...
Text Solution
|
- एक स्वचालित वाहन की बैटरी से इसकी चालन मोटर को जोड़ने वाले तारों में 30...
Text Solution
|
- 1.5 T का एकसमान चुंबकीय क्षेत्र 10.0 सेमी० त्रिज्या के बेलनाकार क्षेत्...
Text Solution
|
- घनात्मक z -दिशा में 3000 G का एक एकसमान चुंबकीय क्षेत्र लगाया गया हैं।...
Text Solution
|
- एक वृत्ताकार कुंडली जिसमे 20 फेरे हैं और जिसक त्रिज्या 10 समी हैं, एकस...
Text Solution
|
- एक परिनालिका जो 60 समी० लम्बी है, जिसकी त्रिज्या 4.0 समी० है और जिसमे ...
Text Solution
|
- किसी गलवानोमेटेर की कुंडली का प्रतिरोध 12omega है। 3 mA की विघुत धारा ...
Text Solution
|
- किसी गलवानोमेटेर की कुंडली का प्रतिरोध 15Omega है। 4mA की विघुत धारा ...
Text Solution
|