Home
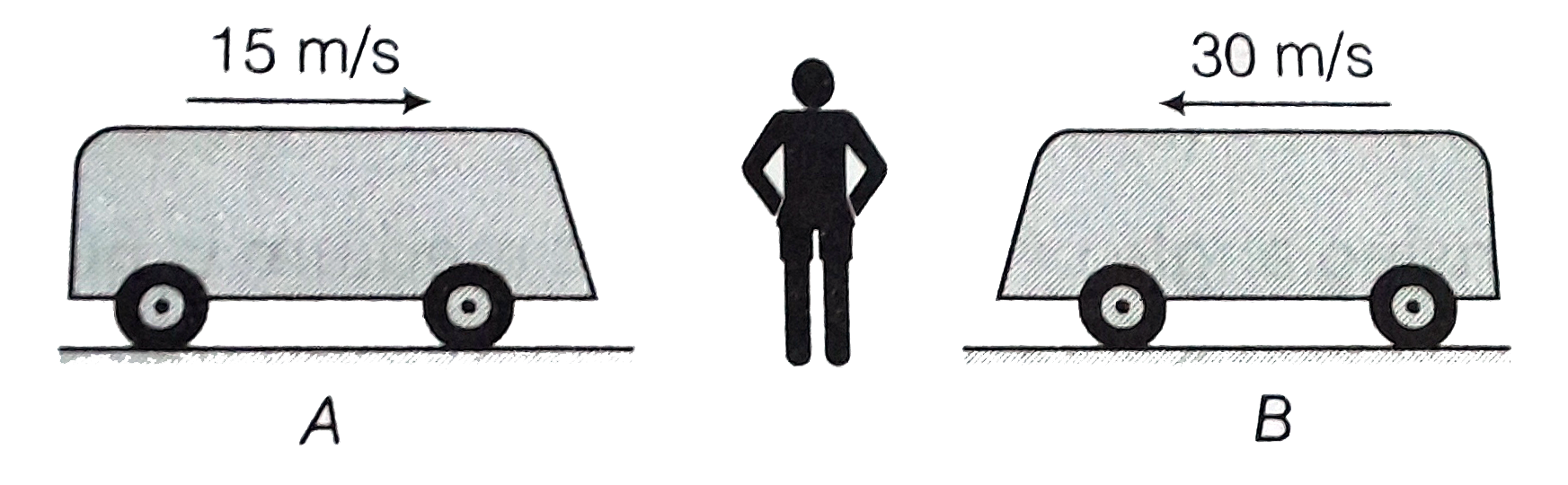
Class 12
PHYSICS
Two cars A and B approach a statinary ob...

Two cars A and B approach a statinary observer from opposite sides as shown in figure. Observer hears no beats. If the frequency of the horn of the car B is 504 Hz, the frequency of horn of car A will be

A

529.2 Hz

B

295.2Hz

C

440.5Hz

D

259.2Hz

Text Solution

Verified by Experts

The correct Answer is:
A
From Doppler's effect, the apparent change in frequency of a wave that is perceived by stationary observer is
`n'=n_(0)((v)/(v-v_(S)))`
where, v is speed of sound. Since, observer is not hearing any beats, observer is not hearing any beats, the apparent frequency of the two cars should be equal.
`thereforen'=n"`
`504((v)/(v-30))=n((v)/(v-15))`
`thereforen=((330-15)xx504)/((330-30))`
`=(315xx504)/(300)=529.2Hz`
Promotional Banner

Topper's Solved these Questions

  • PRACTICE SET 03

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise PAPER 2 (MATHEMATICS)|1 Videos

  • PRACTICE SET 02

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise Paper 1 (Physics)|50 Videos

  • PRACTICE SET 04

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise PAPER 1 (PHYSICS & CHEMISTRY)|50 Videos

Similar Questions

Explore conceptually related problems

Two trains A and B approach a station from opposite sides, sounding their whistles. A stationary observer on the platform hears no beats. If the velocities of A and B are 15 m/s and 30 m/s respectively and the real frequency of the whistle of B is 600 Hz, find the real frequency of the whistle of A. (Velocity of sound = 330 m/s)

A train A is travelling at a speed of 108 km hr^(-1) The train approaches another train B standing on the platform.The engine of the train B below its horn. The frequency of the horn as observed by the driver in train A is 504 Hz. The frequency of the horn of train B is (speed of sound = 330 ms ^(-1)

A toy-car, blowing its horn, is moving with a steady speed of 5 m//s, away from a wall. An observer, towards whom the toy car is moving, is able to heat 5 beats per second. If the velocity of sound in air is 340 m/s, the frequency of the horn of the toy car is close to :

A car has two horns having a difference in frequency of 180 Hz. The car is approaching a stationary observer with a speed of 60 ms^(-1) . Calculate the difference in frequencies of the notes as heard by the observer, If velocity of sound in air is 330 ms^(-1) .

Car X and Car Y approaching each other. Frequency heard by car Y is 1320 Hz. Then, find actual frequency.

Two cars A and B are moving away from each other in opposite directions. Both the cars are moving with a speed of 20 ms^(-1) with respect to the ground. If an observer in car A detects a frequency 2000 Hz of the sound coming from car B, what is the natural frequency of the sound source in car B? (Speed of sound in air = 340 ms^(-1) )

Two cars P and Q are approaching each other with velocities of 36 km/h and 72 km/h respectively. The frequency of a note emitted by car P as heard by the person sitting in car Q is 850 Hz. What will be the frequency of note heard by person sitting in car P ? Velocity of sound = 340 m/s.

At a point, beats frequenc of n Hz is observed it means:

The frequency of the sound of a car horn as recorded by an observer towards whom the car is moving differs from the frequency of the horn by 10% . Assuming the velocity of sound in air to be 330ms^(-1) , the velocity of the car is