Home
Class 12
MATHS
The area bounded by the parabola y^(2)=8...

The area bounded by the parabola `y^(2)=8x,` the x-axis and the latusrectum, is

A

`16//3`

B

`32//3`

C

`8//3`

D

`64//3`

Text Solution

Verified by Experts

The correct Answer is:
B
Equation of latusrectum of the parabola `y^(2)=8x` is x = 2.
Therefore,
Required area `=2int_(0)^(2)sqrt(8x)dx=4sqrt(2)[(x^(3//2))/(3//2)]_(0)^(2)`

`=4sqrt(2)[(2sqrt(2))/(3//2)]=(32)/(3)` sq units
Promotional Banner

Topper's Solved these Questions

  • APPLICATIONS OF DEFINITE INTEGRALS

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise Exercise 2|34 Videos

  • APPLICATIONS OF DEFINITE INTEGRALS

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|6 Videos

  • APPLICATIONS OF DERIVATIVES

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|21 Videos

Similar Questions

Explore conceptually related problems

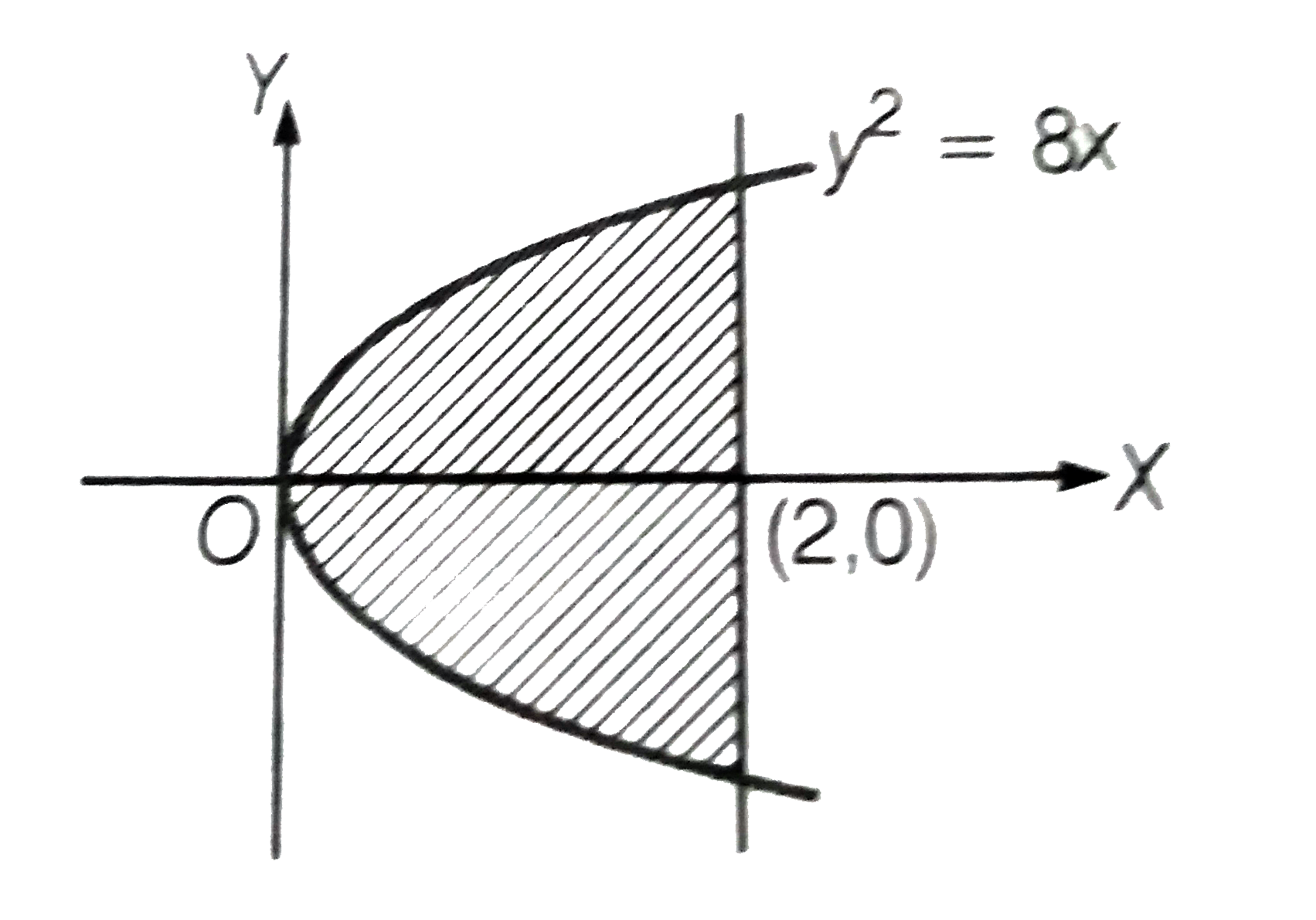
The area bounded by the parabola y^(2) = 32x the X-axis and the latus rectum is …….. sq. units

Area bounded by the parabola ay^(2)=x , the X-axis and the ordinate at x = a is

The area bounded by the parabola y=x^2-7x+10 and X-axis

Find by the method of integration the area of the region bounded by the parabola y^2=8x and its latus rectum.

Area of the region bounded by the parabola ay=x^(2) , the X-axis and the ordinates at x = a, x = 2a is

The area bounded by the parabola y = 4x - x^(2) and X-axis is

The area bounded by the parabola y^(2) = x along the X- axis & the lines x =0 , x= 2 is …… sq. units.

Find the area of the region bounded by the parabola y^2 = 4x , the x-axis, and the lines x = 1 and x = 4.

Find the area bounded by the parabola x^(2) = y , x-axis and the line y = 1