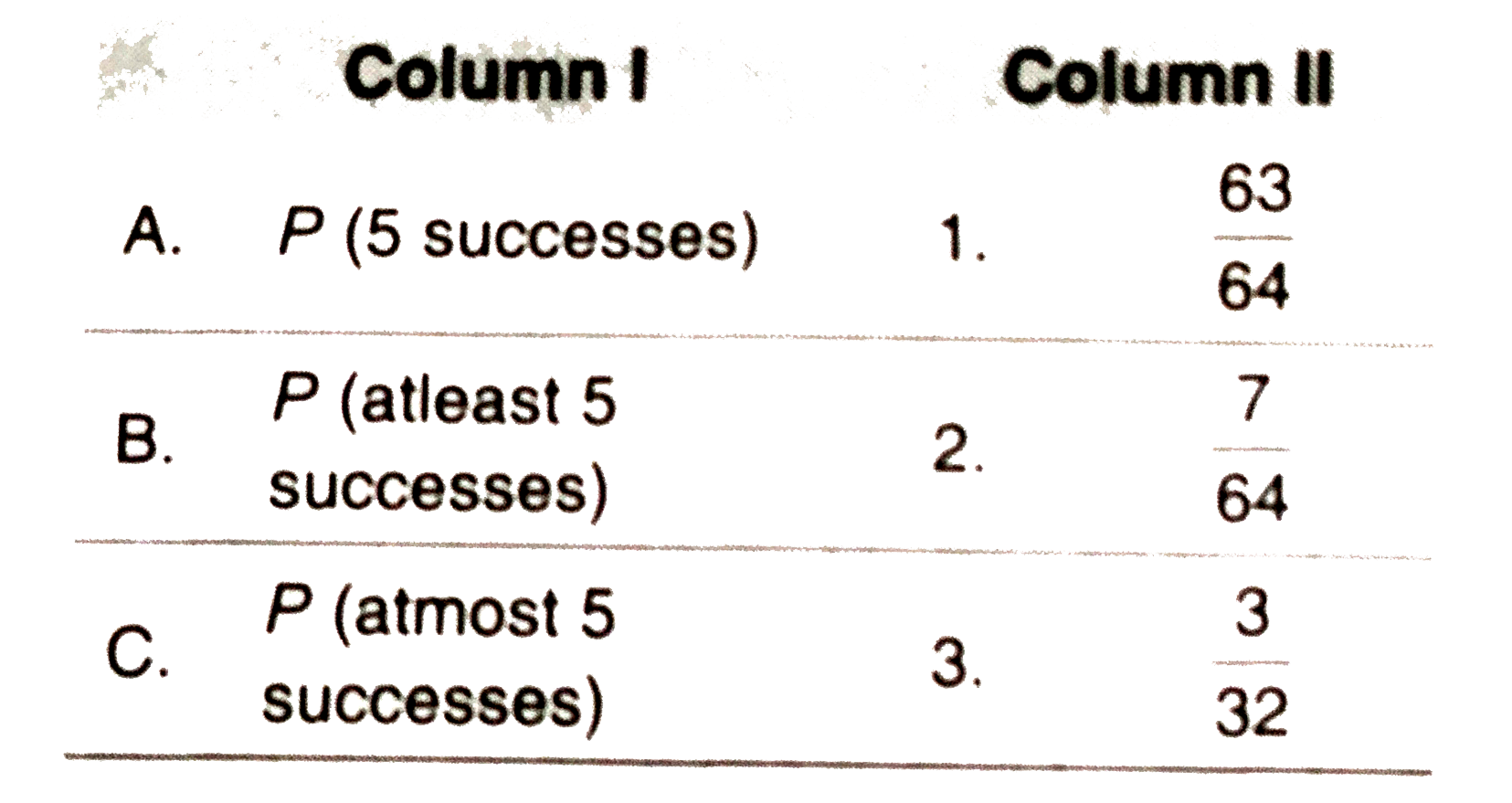A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
BINOMIAL DISTRIBUTION
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise Exercise 1 (Topical problems) (Mean and Variance|7 VideosBINOMIAL DISTRIBUTION
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise Exercise 2 (MISCELLANEOUS PROBLEM) (Mean and Variance|32 VideosAPPLICATIONS OF DERIVATIVES
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|21 VideosCIRCLE AND CONICS
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise All Questions|74 Videos
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-BINOMIAL DISTRIBUTION-MHT CET Corner
- A dice is thrown 6 times. If 'getting an old number' is a success, the...
Text Solution
|
- Let X~B(n,p), if E(X)=5,Var(X)=2.5 then P(X lt 1) is equal to
Text Solution
|
- Probability of guessing correctly atleast 7 out of 10 answers in a 'T...
Text Solution
|
- If random variable X~B(n=5,P=(1)/(3)), then P(2 lt X lt 4) is equal to
Text Solution
|
- 15 coins are tossed , the probability of getting heads will be
Text Solution
|
- If X follows the binomial distribution with parameters n=6 and p and 9...
Text Solution
|
- Two coins are tossed simultaneously. Then, the value of E(X), where X ...
Text Solution
|