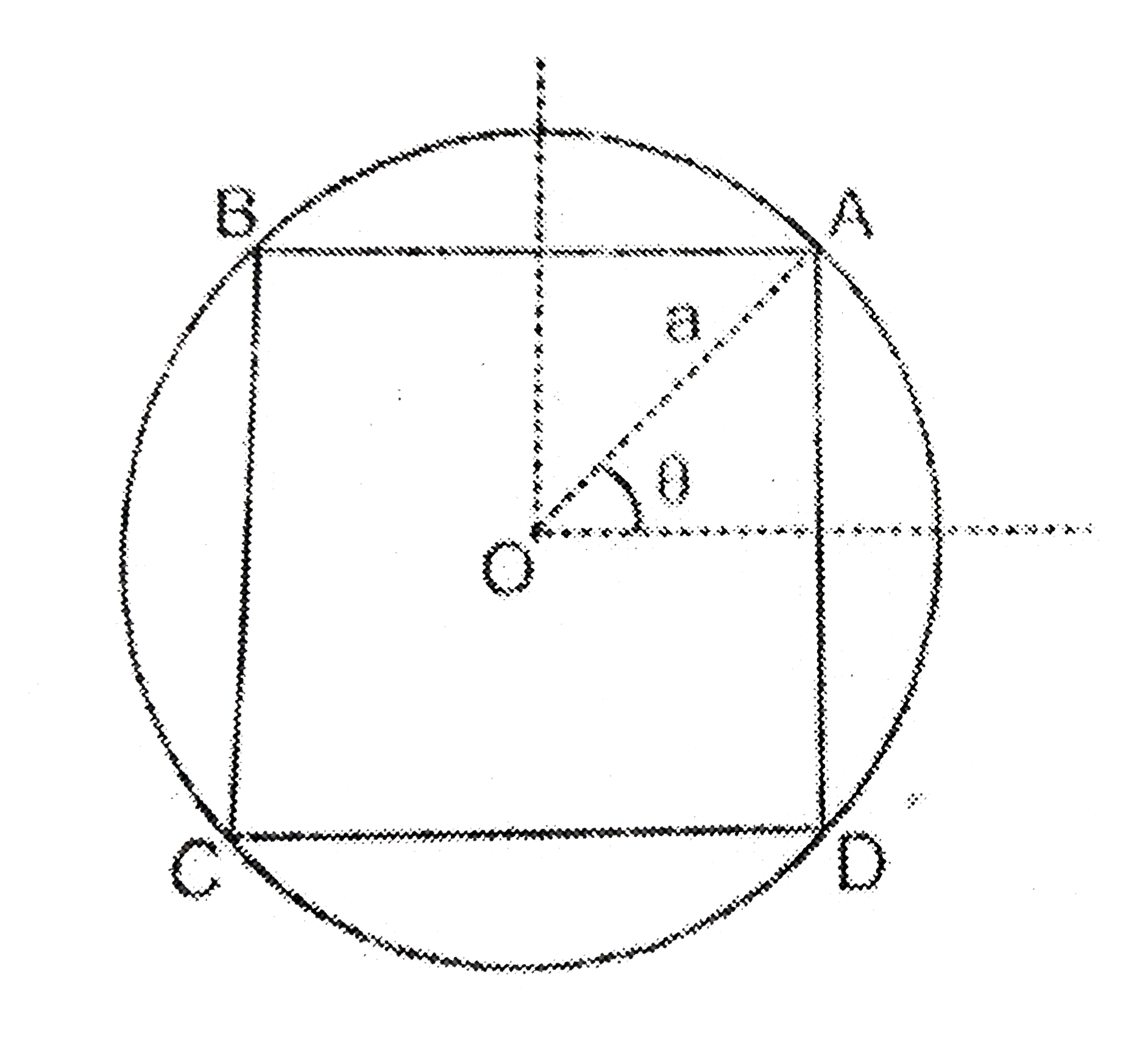
मानलो की वृत का केंद्र मूलबिंदु और वृत की त्रिज्या a है।
`therefore`वृत का समीकरण `x^(2)+y^(2) =a^(2) `
वृत्त के अंतग्रत एक आयत ABCD है स्पष्टतः A के निर्देशांक `(acos0,asin0)` है। मान लीजिए आयत का क्षेत्रफल S है, तो
`" " S=ABxxAD `
`" "=2asin 0,2acos0`
`" "2a^(2) sin 20`
अब अवकलन करने पर `(dS)/(d0)=0`प्रतिस्तापित करने पर
`" " 4a^(2) cos20=0" "` या `" " cos 20=0=cos""(pi)/(2)`
` rArr " " 20=(pi)/(2) " "` या `" " 0=(pi)/(4)`
पुनः अवकलन करने पर,
`" " (d^(2) S) /(d0^(2)) =-4a^(2) 2sin 20=-8a^(2) sin 20 `
`therefore0=(pi)/(4)`रखने पर ltbgt`" "( d^(2) S) /(d0^(2)) =-8a^(2) sin 2((pi)/(4))=-8a^(2) sin ""(pi)/(2) =-8a^(2) `ऋणात्मक
`therefore`जब `0=(pi)/(4),AB=2asin 0=2asin ""(pi)/(4) =sqrt(2a)`
और `" " AD =2acos0=2acos""(pi)/(4) =sqrt(2a) " "therefore AB =AD ` अतः जब आयत का क्षेत्रफल उच्चिष्ट होगा तब आयत एक वर्ग है।
दूसरी विधि - मान लीजिए की आयत की भुजाये x तथा y है। A उसका क्षेत्रफल है और वृत की त्रिज्या a है।
`therefore " "A=xy `
और वृत का समीकरण `" "x^(2)+y^(2) =a^(2) `
समीकरण (i ) और (ii ) से
`" " A=xsqrt(a^(2)-x^(2)`
A महत्तम होगा जब `(dA)/(dx) =0`और `(d^(2)A)/(dx^(2)) =-ve ` (ऋणात्मक )
अब `" "(dA)/(dx) =sqrt(a^(2)-x^(2) )।1+x(1)/(2) (a^(2)-x^(2) ) ^(-1//2) (-2x)=0`
`rArr " " (a^(2) -x^(2) -x^(2) )/sqrt(a^(2)-x^(2))=0therefore x=+-(a)/sqrt(2)`
`rArr" " x=(a)/sqrt(2)`
और `(d^(2)A)/(dx^(2)) =(sqrt(a^(2)-x^(2))(-4x)-(a^(2)-2x^(2)))*(1)/(2) (a^(2) -x^(2) )^(-1//2)(-2x))/(a^(2) -x^(2) `
`(d^(2)A)/dx^(2) ` का मान `x=(a)/sqrt(2)` के लिए ऋणात्मक है।
`therefore" "` जब `x=(a)/sqrt2,y=sqrt(a^2-x2) =sqrt(a^(2)-a^(2)/2)=(a)/sqrt2`
अतः क्षेत्रफल महत्तम होगा जब x =y अर्थात आयत एक वर्ग होगा।