लिखित उत्तर
Verified by Experts
MANOHAR RAY-अवकलन के अनुप्रयोग -इंजीनियरिंग परीक्षाओं के प्रश्न
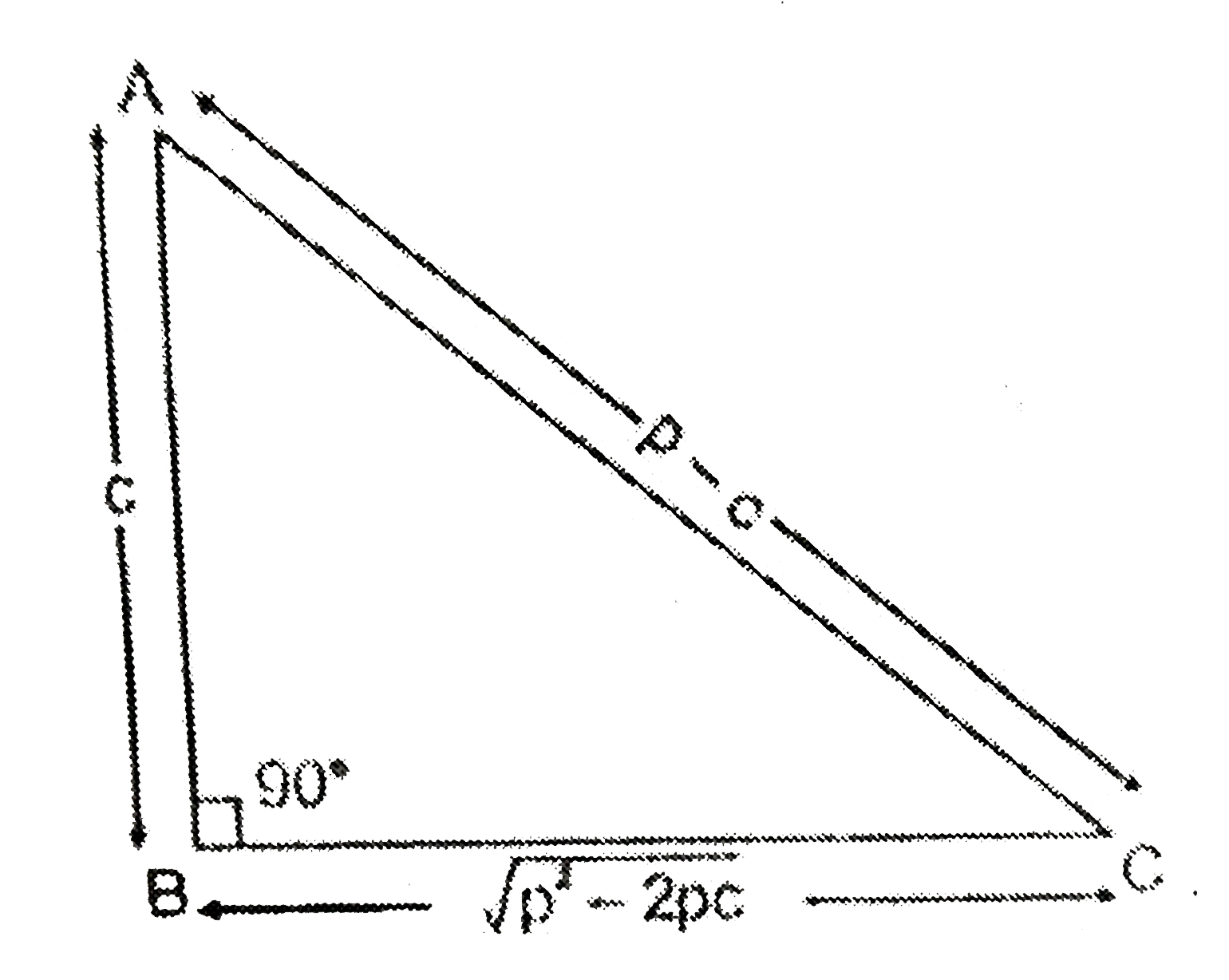
- यदि एक समकोण त्रिभुज के कर्ण और एक भुजा की लम्बाइयों का योग दिया हो, त...
Text Solution
|
- एक गोलाकार गुब्बारे में 4500piघन मी हीलियम गैस भरी गई है। यदि गुब्बारे...
Text Solution
|
- वक्र y=x+(4)/(x^(2)) की स्पर्श रेखा, जो x अक्ष के समांतर है, का समीकर...
Text Solution
|
- एक तार की लम्बाई 2 इकाई है। इसके दो भाग किये गए, पहले भाग x इकाई का एक...
Text Solution
|
- A,B,C तीन शहरों में किसी कंपनी की तीन ब्रांच है।A तथा B के बीच की दुरी...
Text Solution
|
- अंतराल [-sqrt(13),sqrt13 ] में स्थित उन बिन्दुओ की संख्या ज्ञात करो जि...
Text Solution
|
- बिंदु (1 ,1 ) से वक्र f(x)=x^(2) +bx-bपर खींची गई स्पर्श रेखाओं तथा अक...
Text Solution
|