When a parallel beam of monochromatic light (wavelength `lambda`) illuminates a single slit of finite width `a (a gt gt lambda)`, we observe on a screen some distance from the slit a broad pattern of alternate dark and bright fringes. The pattern consists consists of a central bright fringe, with successive dark and bright fringes of diminishing intensity on both sides. This is called the diffraction pattern of a single slit.
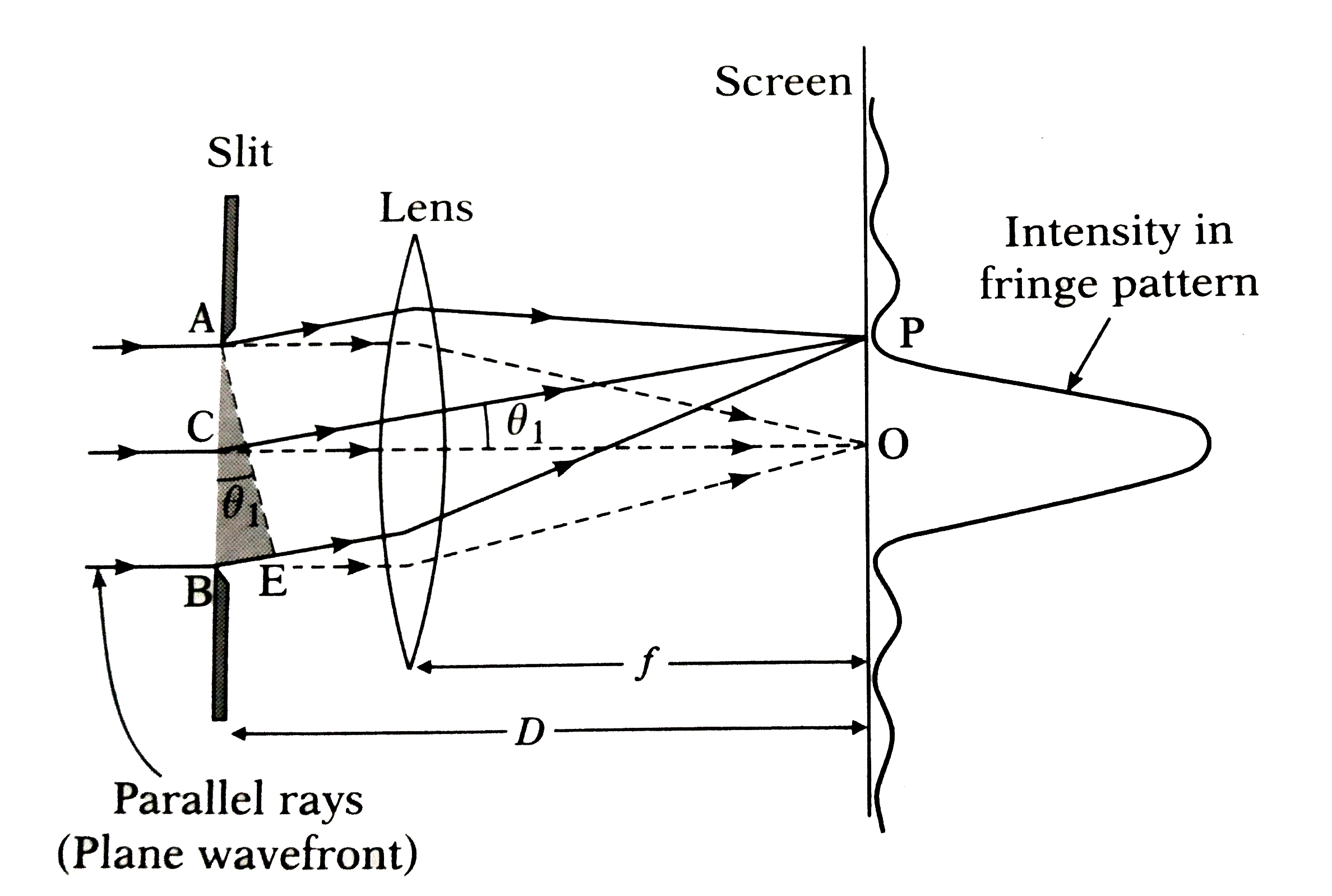
Consider a single slit illuminated with a parallel beam of monochromtic light perpendicular to the plane of the slit. The diffraction pattern is obtained on a screen at a distance D(gtgta) from the slit and at the focal plane of the convex lens.
We can imagine the single slit as made up of a large number of Hugens sources evenly distributed over teh width of the slit. Then, the maxima and minima of the pattern arise from the interference of the various Huygens wavelets.
Now, imagine the single slit as being made up of two adjacent slits, each of width a/2. Since the incident plane wavefronts are parallel to the plane of the slit, all the Huygens sources at the slit will be in phase. They will therefore also be in phase at the point O on the screen, where O is equidistant from all the Hugens sources. At O, then, we get the central maximum.
For the first minimum of intensity on the screen, the path difference between the waves from the Huygens sources A and C (or C and B) is `lambda//2`, which is the condition for destructive interference. Suppose the nodal line CP for the first minimum subtends an angle `theta_(1)` at the slit, `theta_(1)` is very small.
With P as the centre and PA as radius, strike an arc intersecting PB at E. Since D gtgt a, the arc AE can be considered a straight line at right angles to PB. Then `triangle ABE` is a right-angled triangle similar to `triangle COP.`
This means that `angle BAE=theta_(1).`
`therefore BE=a sin theta_(1).`
But BE is the difference in path length, PB - PA.
`therefore BE=PB-PA=(PB-PC)+(PC-PA)`
`=(lambda)/(2)+(lambda)/(2)=lambda`
`therefore a sin theta_(1)=lambda`
`therefore sin theta_(1) ~= theta_(1)=(lambda)/(a) " "( because theta_(1) " is very small and in radian") " " ` ...(1)
The other nodal lines of intensity minima can be understood in a similar way. In general, then, for the mth minimum `(m=pm1, pm2, pm3, ...)`,
`theta_(m)=(m lambda)/(a) " (mth minimum) " ` ...(2)
Between the above successive minima, the intensity rises to secondary maxima when the path difference is odd integral multiple of `(lambda)/(2)`:
`a sin theta_(m) =(2m+1)(lambda)/(2)=(m+(1)/(2))lambda`
i.e., at angles given by
`theta_(m) ~= sin theta_(m) =(m+(1)/(2))(lambda)/(a) " (mth secondary maximum) " ` ...(3)
