Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTRIC CURRENT THROUGH GASES
HC VERMA|Exercise Objective 2|7 VideosELECTRIC CURRENT THROUGH GASES
HC VERMA|Exercise Exercises|23 VideosELECTRIC CURRENT THROUGH GASES
HC VERMA|Exercise Short Answer|10 VideosELECTRIC CURRENT IN CONDUCTORS
HC VERMA|Exercise Exercises|84 VideosELECTRIC FIELD AND POTENTIAL
HC VERMA|Exercise Exercises|75 Videos
Similar Questions
Explore conceptually related problems
HC VERMA-ELECTRIC CURRENT THROUGH GASES-Objective 1
- Cathode rays constitute a stream of
Text Solution
|
- Cathode rays passing through a discharge tube. In the tube, there is
Text Solution
|
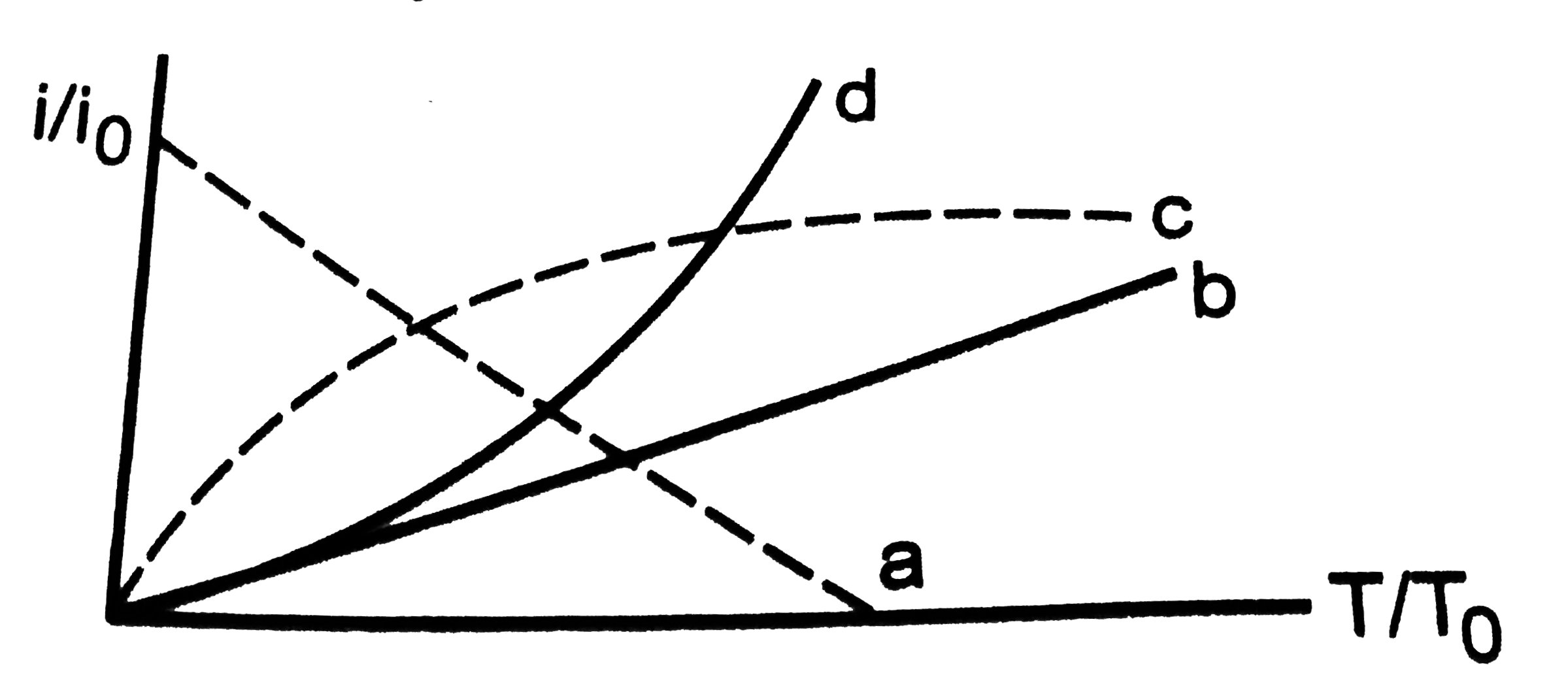
- Let i0 be the thermionic current from a metal surface when the absolut...
Text Solution
|
- When the diode shows saturated current, dynamic plate resistance is
Text Solution
|
- The anode of a thermionic diode is connected to the negative terminal ...
Text Solution
|
- A diode, a resistor and a 50 Hz AC source are connected in series. The...
Text Solution
|
- A triode is operated in the liner region of its characteristics. If th...
Text Solution
|
- The plate current in a triode valve is maximum when the potential of t...
Text Solution
|
- The amplification factor of a triode operating in the linear region de...
Text Solution
|