Text Solution
Verified by Experts
Topper's Solved these Questions
RS AGGARWAL-VOLUME AND SURFACE AREAS OF SOLIDS-MULTIPLE-CHOICE QUESTIONS(MCQ)
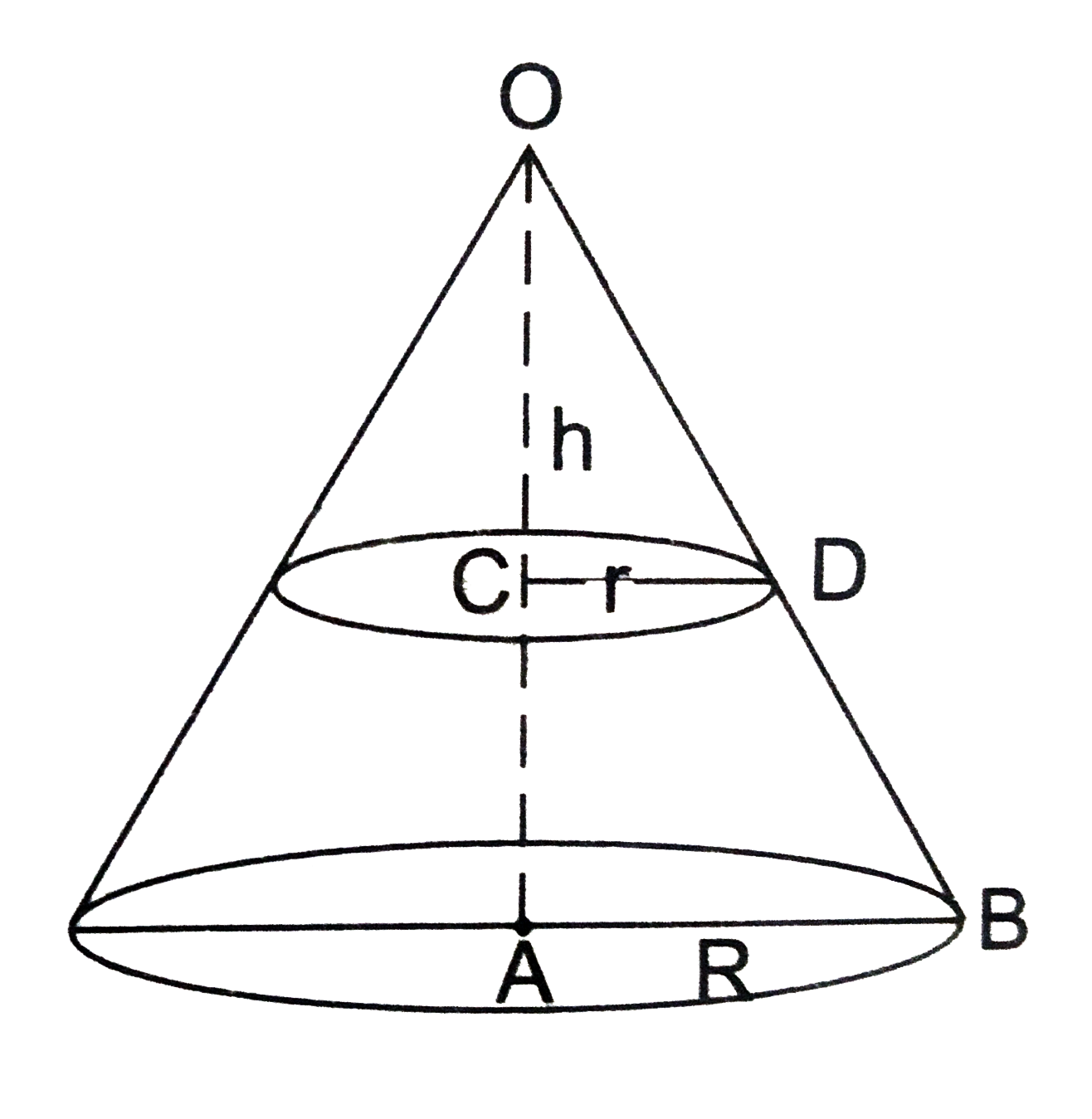
- The height of a cone is 30 cm. A small cone is cut off at the top b...
Text Solution
|
- A shulltlecock used ofor playing badmintion is the combination of
Text Solution
|
- A funnel is the combination of
Text Solution
|
- A surahi is a combination of
Text Solution
|
- The shape of a glass (tumbler) is usually in the form of
Text Solution
|
- The shape of a gilli in the gilli-danda game is a combination of
Text Solution
|
- A plumbline (sahul) is the combination of
Text Solution
|
- A cone is cut by a plane parallel to its base and the upper part is re...
Text Solution
|
- Match the following columns:
Text Solution
|
- Match the following columns:
Text Solution
|
- Which of the following is correct
Text Solution
|
- The correct answer a/b/c/d
Text Solution
|
- The correct answer a/b/c/d
Text Solution
|
- The correct answer a/b/c/d
Text Solution
|
- The correct answer a/b/c/d
Text Solution
|