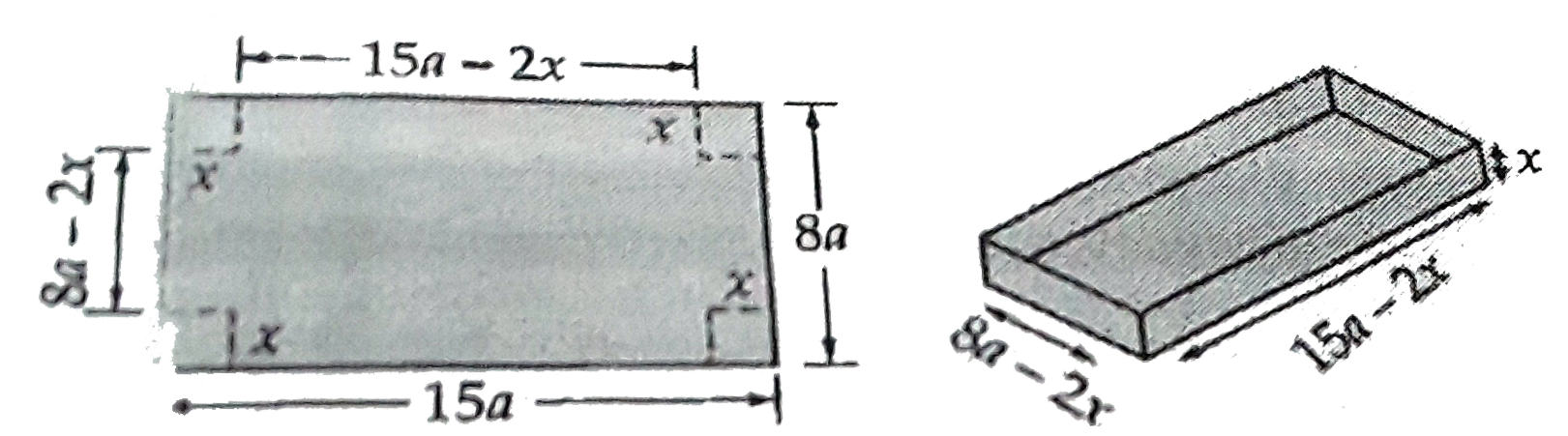
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MAXIMA AND MINIMA
OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|7 VideosMAXIMA AND MINIMA
OBJECTIVE RD SHARMA|Exercise Exercise|50 VideosMAXIMA AND MINIMA
OBJECTIVE RD SHARMA|Exercise Chapter Test|30 VideosMATHEMATICAL REASONING
OBJECTIVE RD SHARMA|Exercise Chapter Test|20 VideosMEASURES OF CENTRAL TENDENCY
OBJECTIVE RD SHARMA|Exercise Chapter Test|21 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA-MAXIMA AND MINIMA -Section I - Solved Mcqs
- If alpha and beta respectively the minmum and minimum values of the fu...
Text Solution
|
- Let f(x)={{:(x^2+4x "," -3 le x le 0),(-sin x ","0 lt x le pi//2 ),(...
Text Solution
|
- If alpha be the number of solutions of the equation [sin x] =|x| ) and...
Text Solution
|
- Let f(x1,x2,x3,x4)=x1^2+x2^2+x3^2+x4^2-2(x1+x2+x3+x4)+10 and x1,x3 i...
Text Solution
|
- Let f,g and h be real-valued functions defined on the interval [0,1] b...
Text Solution
|
- Let f be a function defined on R (the set of all real numbers) such th...
Text Solution
|
- Let f:R to R be defined by f(x)={{:(2k-2x",",ifxle-1),(2x+3",",iffxg...
Text Solution
|
- For e in (0,(5pi)/(2)) " define " f(x)= int(0)^(x) sqrt(t) sin t dt ...
Text Solution
|
- Let p(x) be a real polynomial of least degree which has a local maximu...
Text Solution
|
- Let I RvecI R be defined as f(x)=|x|++x^2-1|dot The total number of po...
Text Solution
|
- If f(x) = int(0)^(x) e^(t^2)(t-2)(t-3) dt " for all " x in (0,oo) t...
Text Solution
|
- The function f(x)=2|x|+|x+2|=||x|2|-2|x|| has a local minimum or a loc...
Text Solution
|
- Let f:[0,1] rarr R be a function . Suppose the fuction f is twice diff...
Text Solution
|
- Let f:[0,1] rarr R be a function.such that f(0)=f(1)=0 and f''(x)+f(x...
Text Solution
|
- A rectangular sheet of fixed perimeter with sides having their lengths...
Text Solution
|
- Let f(x) be a polynomial of degree four having extreme vlaues at x=1 ...
Text Solution
|
- A cylindrica container is to be made from certain solid material with ...
Text Solution
|
- The minimum value of the function f(x)=x^(3//2)+x^(-3//2)-4(x+1/x) ...
Text Solution
|
- The least value of a in RR for which 4ax^2+1/x >= 1, for all x > 0, ...
Text Solution
|
- The abscissae of a point, tangent at which to the curve y = e^x sin x...
Text Solution
|