Home
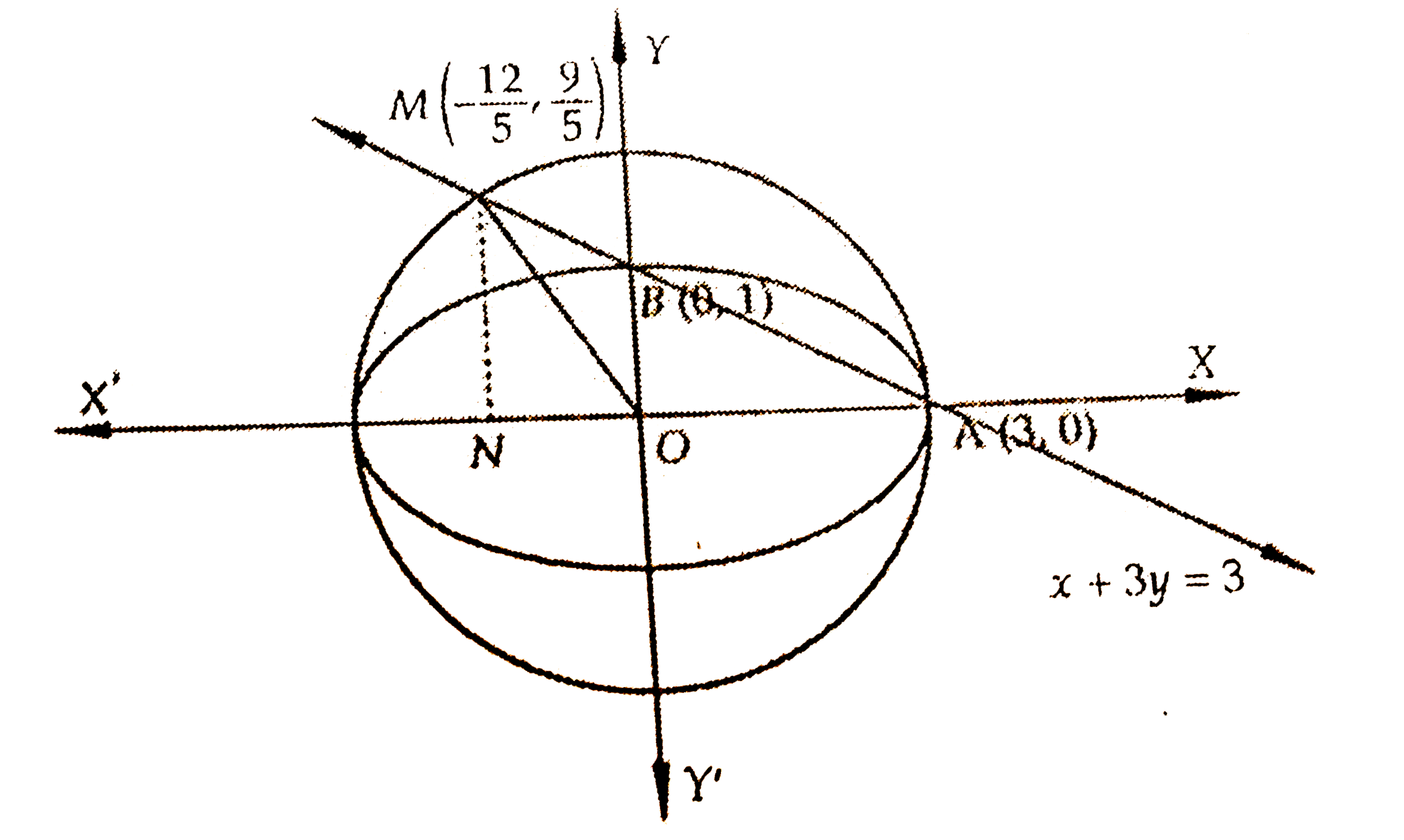
Class 12
MATHS
The line passing through the extremity A...

The line passing through the extremity `A` of the major exis and extremity `B` of the minor axis of the ellipse `x^2+9y^2=9` meets is auxiliary circle at the point `Mdot` Then the area of the triangle with vertices at `A ,M ,` and `O` (the origin) is

A

`31//10`

B

`29//10`

C

`21//10`

D

`27//10`

Text Solution

Verified by Experts

The correct Answer is:
D
The coordinate of A and B are (3,0) and (0,1) respectivley the auxiliary circle is `x^(2)+y^(2)=9`
Equation of line AB is `(x)/(3)+(y)/(1) =1 or x+3y=3` this cuts the auxiliary circle at `M(-12//5,9//5)`
` therefore ` Area of `Delta AOM =(1)/(2) xxOA xxMN =(1)/(2) xx3xx(9)/(5)=(27)/(10)`
Promotional Banner

Topper's Solved these Questions

  • ELLIPSE

    OBJECTIVE RD SHARMA|Exercise Section I - Solved Mcqs|59 Videos

  • ELLIPSE

    OBJECTIVE RD SHARMA|Exercise Section II - Assertion Reason Type|7 Videos

  • DIFFERENTIATION

    OBJECTIVE RD SHARMA|Exercise Chapter Test|30 Videos

  • EXPONENTIAL AND LOGARITHMIC SERIES

    OBJECTIVE RD SHARMA|Exercise Chapter Test|20 Videos

Similar Questions

Explore conceptually related problems

The line passing through the extremity A of the major exis and extremity B of the minor axis of the ellipse x^(2)+9y^(2)=9 meets is auxiliary circle at the point M. Then the area of the triangle with vertices at A,M, and O (the origin) is 31/10(b) 29/10(c) 21/10 (d) 27/10

The line passing through the extremity A of the major axis and extremity B of the minor axis of the ellipse x^(2) + 16y^(2) = 16 meets its auxiliary circle of the point M. Then the area of the triangle with vertices of A, M and the origin O is ____________ .

The line passing through the " extremity "A" of the major axis and extremity "B" of the minor axis of the ellipse x^(2)+9y^(2)=9 ," meets its auxiliary circle at the point "M" Then the integer closest to the area of the triangle with "vertices at "A,M" and the origin O is

The line passing through the extremity A of major axis and extremity B of the minor axes of the ellipse 9x^2 + 16y^2 = 144 meets the circle x^2+ y^2 =16 at the point P. Then the area of the triangle OAP, O being the origin (in square units) is

Lines x+y=1 and 3y=x+3 intersect the ellipse x^(2)+9y^(2)=9 at the points P,Q,R. the area of the triangles PQR is

The vertices of a quadrilateral are situated at foci and the extrimities of the minor axis of the ellipse 4x^(2) + 9y^(2) = 36 . Find the area of the quadrilateral .

OBJECTIVE RD SHARMA-ELLIPSE-Chapter Test
  1. The line passing through the extremity A of the major exis and extremi...

    Text Solution

    |

  2. Find the maximum area of an isosceles triangle inscribed in the ellip...

    Text Solution

    |

  3. A tangent to the ellipse x^2+4y^2=4 meets the ellipse x^2+2y^2=6 at P&...

    Text Solution

    |

  4. If the distance of a point on the ellipse (x^(2))/(6) + (y^(2))/(2) = ...

    Text Solution

    |

  5. If the minor axis of an ellipse subtends an angle of 60^(@) at each fo...

    Text Solution

    |

  6. Let Sa n dS ' be two foci of the ellipse (x^2)/(a^3)+(y^2)/(b^2)=1 . I...

    Text Solution

    |

  7. The equation of the normal at the point P (2, 3) on the ellipse 9x^(2)...

    Text Solution

    |

  8. For the ellipse 3x^(2) + 4y^(2) + 6x - 8y - 5 = 0 the eccentrically, i...

    Text Solution

    |

  9. Let S, S' be the focil and BB' be the minor axis of the ellipse (x^(2)...

    Text Solution

    |

  10. If the length of the latusrectum of the ellipse x^(2) tan^(2) theta + ...

    Text Solution

    |

  11. if vertices of an ellipse are (-4,1),(6,1) and x-2y=2 is focal chord t...

    Text Solution

    |

  12. If (-4, 3) and (8, 3) are the vertices of an ellipse whose eccentricit...

    Text Solution

    |

  13. The area of the triangle formed by three points on the ellipse x^2/a^2...

    Text Solution

    |

  14. If the chord joining points P(alpha)a n dQ(beta) on the ellipse ((x...

    Text Solution

    |

  15. If P(alpha,beta) is appoint on the ellipse (x^2)/(a^2)+(y^2)/(b^2)=...

    Text Solution

    |

  16. The tangent at any point P on the ellipse meets the tangents at the ve...

    Text Solution

    |

  17. P is a point on the circle x^(2) + y^(2) = c^(2). The locus of the mid...

    Text Solution

    |

  18. The locus of the poles of normal chords of the ellipse x^(2)/a^(2) + y...

    Text Solution

    |

  19. The locus of mid-points of a focal chord of the ellipse x^2/a^2+y^2/b^...

    Text Solution

    |

  20. The locus of points whose polars with respect to the ellipse x^(2)/a^(...

    Text Solution

    |

  21. if the chord of contact of tangents from a point P to the hyperbola x...

    Text Solution

    |