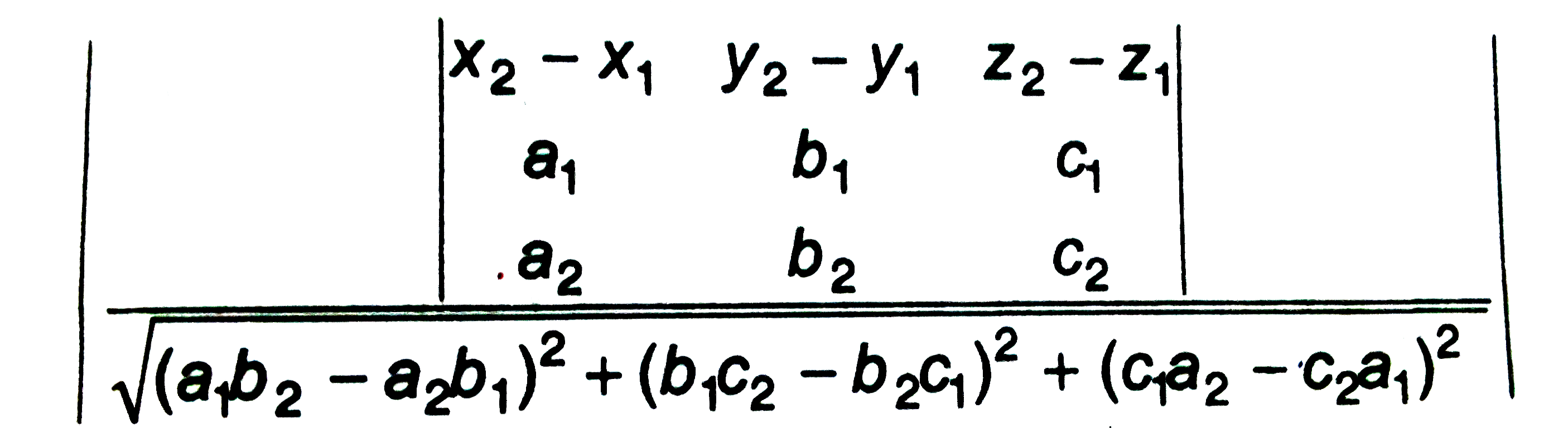A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LINE
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise Exercise 2(Miscellaneous Problems)|30 VideosLINE
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|3 VideosINTEGRATION
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|30 VideosLinear Programming
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|13 Videos
Similar Questions
Explore conceptually related problems
MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-LINE-MHT CET Corner
- The shortest distance between the lines (x-x(1))/(a(1)) =(y-y(1))/(b(1...
Text Solution
|
- Direction cosines of the line (x+2)/(2)=(2y-5)/(3),z=-1 are
Text Solution
|
- The line (x+1)/(-10)=(y+3)/(-1)=(z-4)/1 and (x+10)/(-1)=(y+1)/(-3) =(z...
Text Solution
|
- The symmetric equation of lines 3x+2z-5=0 and x+y-2z-3=0 is
Text Solution
|