Home
Class 11
PHYSICS
At a height of 45 m from ground velocity...

At a height of 45 m from ground velocity of a projectile is,
`v = (30hati + 40hatj) m//s`
Find initial velocity, time of flight, maximum height and horizontal range of this projectile. Here `hati` and` hatj` are the unit vectors in horizontal and vertical directions.

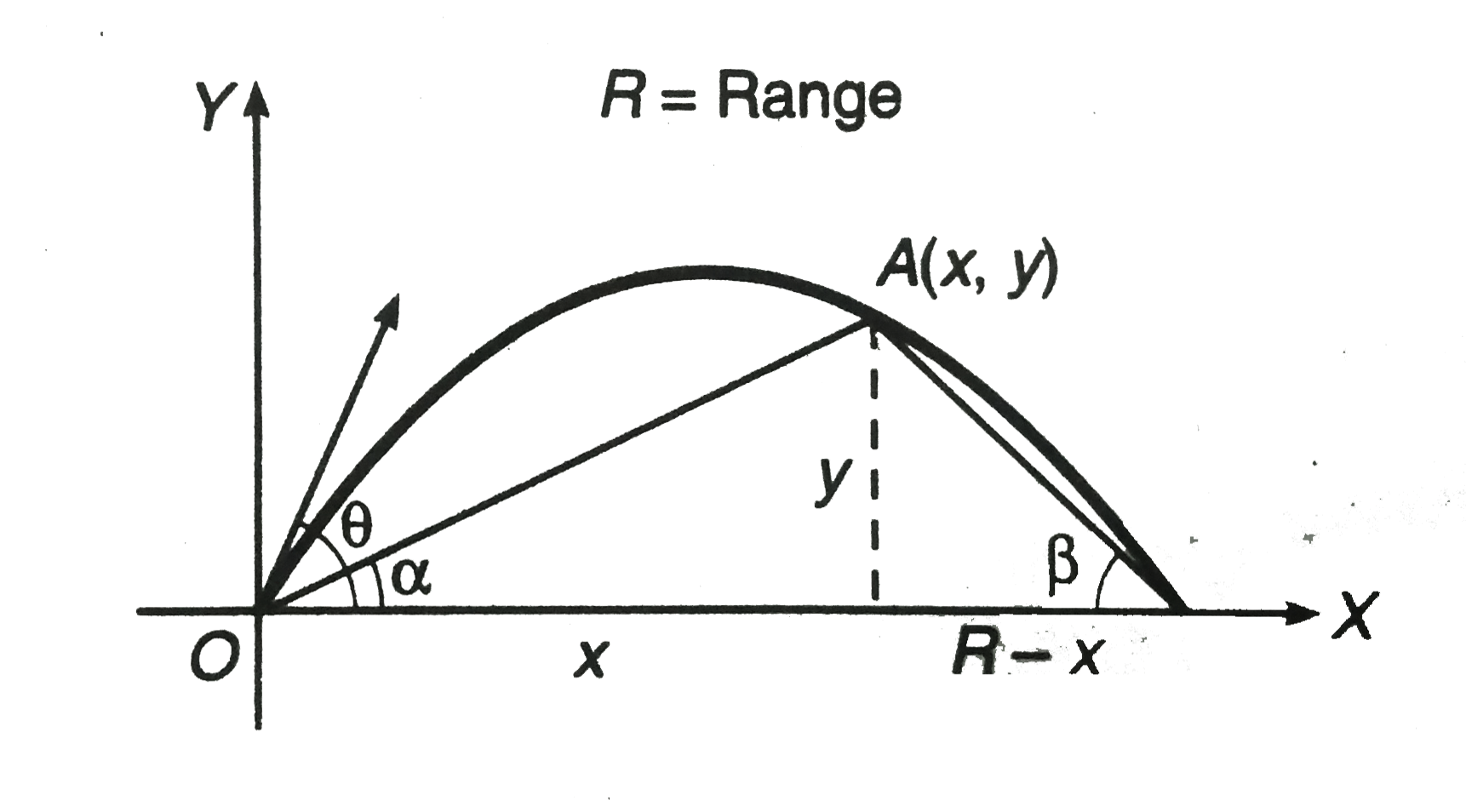
Text Solution

Verified by Experts

The correct Answer is:
A, B, C, D
Given, `v_x = 30m//s and v_y = 40 m//s `
Horizontal component of velocity remains unchanged.
`:. u_x = v_x = 30 m//s`
Vertical component of velocity is more at lesser heights.
Therefore,
`u_ygtv_y`
or `u_y = (sqrt((v_(y)^2)+2 gh))`
` = (sqrt((40)^2 + (2)(10)(45)))`
`= 50 m//s `
Initial velocity of projectile,
`u = (sqrt((u_(x)^2) +(u_(y)^2)))`
`=(sqrt((30)^2 + (50)^2))`
`=10(sqrt34) m//s `
`tan theta = u_y/u_x = 50/30 = 5/3`
` :. theta = tan^-1 (5/3)`
Time of flight, `T = ((2u sin theta)/(g)) = ((2u_y)/g)`
`= ((2xx50)/10)`
= 10s.
Maximum height, `H=(u^(2)sin^(2)theta)/(2g)=(u_(y)^(2))/(2g)`
`=((5)^(2))/(2xx10)=125m`
Horozontal range `R=u_(x)T`
`=30xx10`
`=300 m`
Promotional Banner

Topper's Solved these Questions

  • PROJECTILE MOTION

    DC PANDEY|Exercise Miscellaneous Examples|4 Videos

  • PROJECTILE MOTION

    DC PANDEY|Exercise Exercise 7.1|5 Videos

  • PROJECTILE MOTION

    DC PANDEY|Exercise Example Type 4|1 Videos

  • MOTION IN A PLANE

    DC PANDEY|Exercise (C )Medical entrances gallery|32 Videos

  • PROPERTIES OF MATTER

    DC PANDEY|Exercise Integer|8 Videos

Similar Questions

Explore conceptually related problems

Find the equation of trajectory, time of flight , maximum height and horizontal range of a projectile when projected at an angle theta with the vertical direction .

At a height of 15 m from ground velocity of a projectile is v = (10hati+ 10hatj) . Here hatj is vertically upwards and hati is along horizontal direction then (g = 10 ms^(-1) )

Find (a) time of flight , (b) Max.height (c ) Horizontal range of projectile projected with speed (v) making an angle theta with the horizontal direction from ground.

The velocity of a projectile at the initial point A is (2hati+3hatj) m//s . Its velocity (in m/s) at point B is

The maximum horizontal range of a projectile is 400 m . The maximum value of height attained by it will be

If the horizontal range of a projectile be a and the maximum height attained by it is b, then prove that the velocity of projection is

Assertion At height 20 m from ground , velocity of a projectile is v = (20 hati + 10 hatj) ms^(-1) . Here, hati is horizontal and hatj is vertical. Then, the particle is at the same height after 4s. Reason Maximum height of particle from ground is 40m (take, g = 10 ms^(-2))

From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20" m s"^(-1) The horizontal range of the projectile is