Text Solution
Verified by Experts
Topper's Solved these Questions
WORK, ENERGY & POWER
DC PANDEY|Exercise TYPE2|1 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise Miscellaneous Example|6 VideosWORK, ENERGY & POWER
DC PANDEY|Exercise Level 2 Comprehension Based|2 VideosWAVE MOTION
DC PANDEY|Exercise Integer Type Question|11 VideosWORK, ENERGY AND POWER
DC PANDEY|Exercise MEDICAL ENTRACES GALLERY|33 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-WORK, ENERGY & POWER-Solved Examples
- In the figure shown, all surfaces are smooth and force constant of spr...
Text Solution
|
- A smooth narrow tube in the form of an arc AB of a circle of centre O ...
Text Solution
|
- One end of a light spring of natural length d and spring constant k is...
Text Solution
|
- In the adjoining figure, block A is of mass (m) and block B is of mass...
Text Solution
|
- . In the figure shown, AB = BC = 2m. Friction coefficient everywhere...
Text Solution
|
- A particle slides along a track with elevated ends and a flat central ...
Text Solution
|
- A 0.5kg block slides from the point A on a horizontal track with an in...
Text Solution
|
- A body is desplaced from origin to (2m, 4m) under the following two fo...
Text Solution
|
- A force F=-k(^hati + x^hatj) (where k is a positive constant) acts on ...
Text Solution
|
- A body is displaced from prigin to (1m,1m) by force F=(2yhati + 3x^(...
Text Solution
|
- A particle, which is constrained to move along x-axis, is subjected to...
Text Solution
|
- A particle is placed at the origin and a force F=Kx is acting on it (w...
Text Solution
|
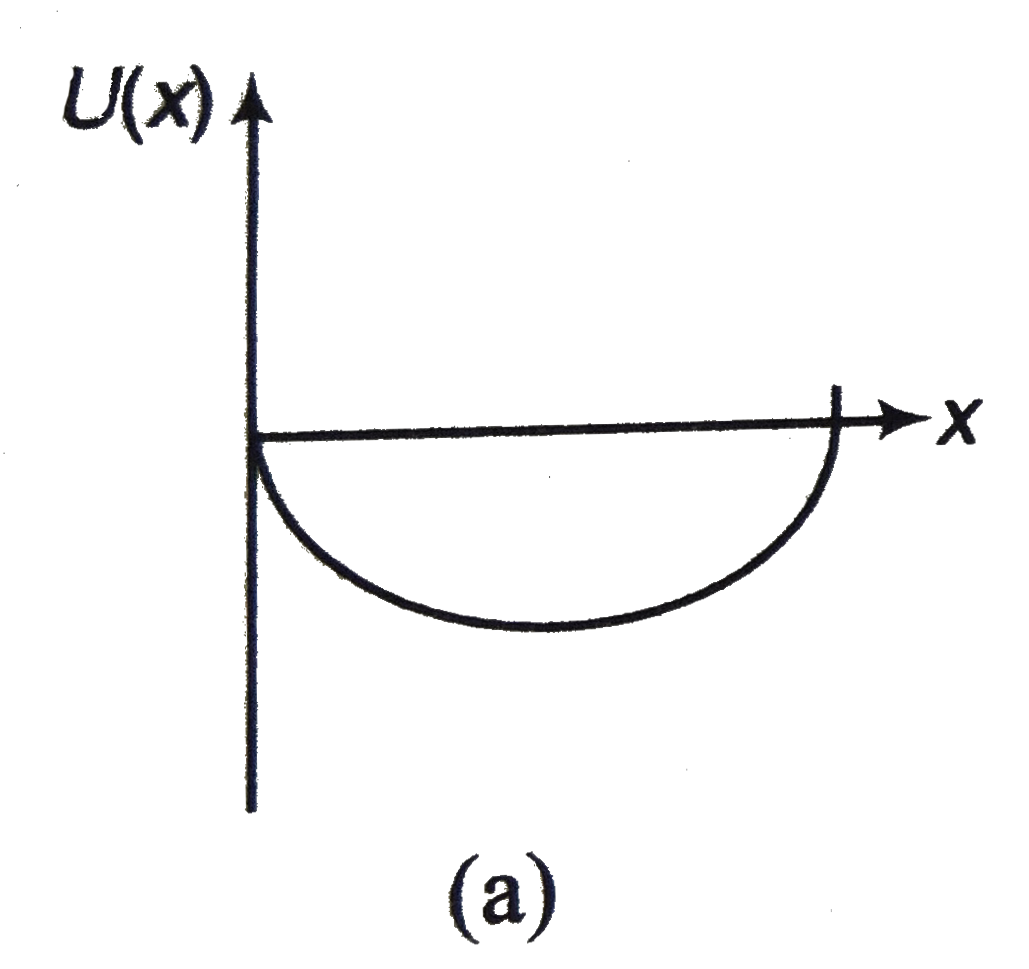 , (b)
, (b) 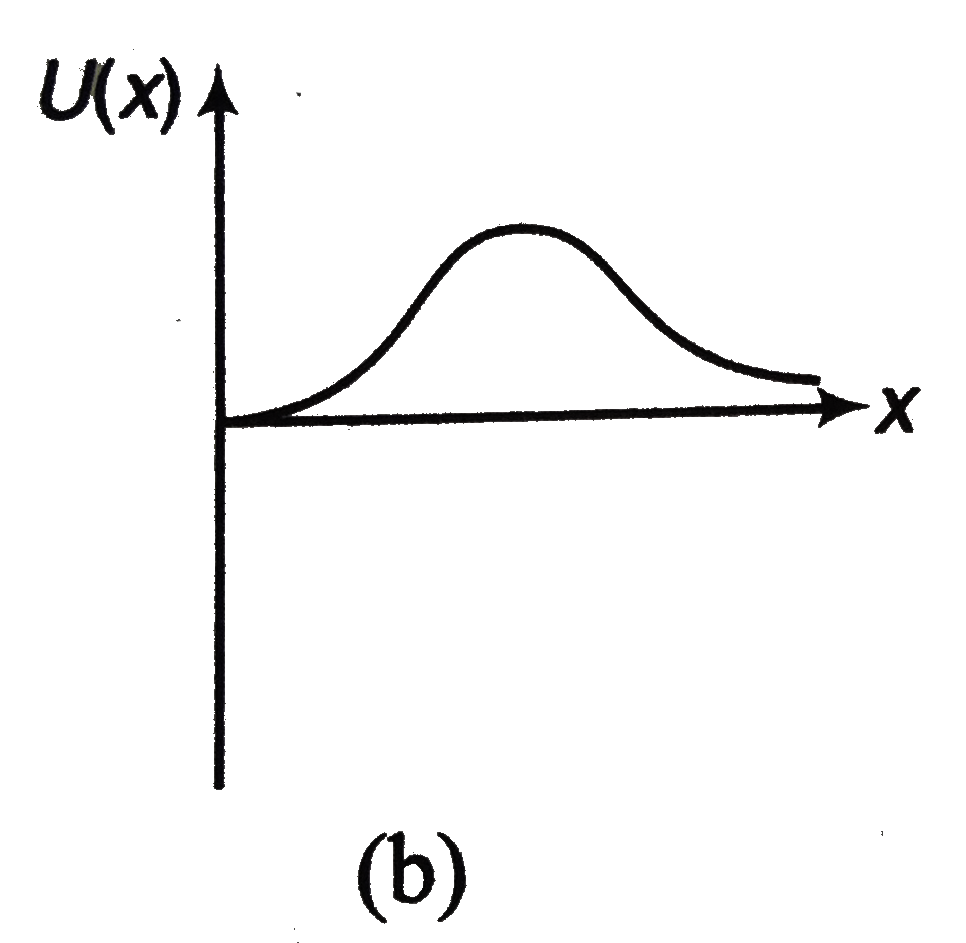 , (c)
, (c) 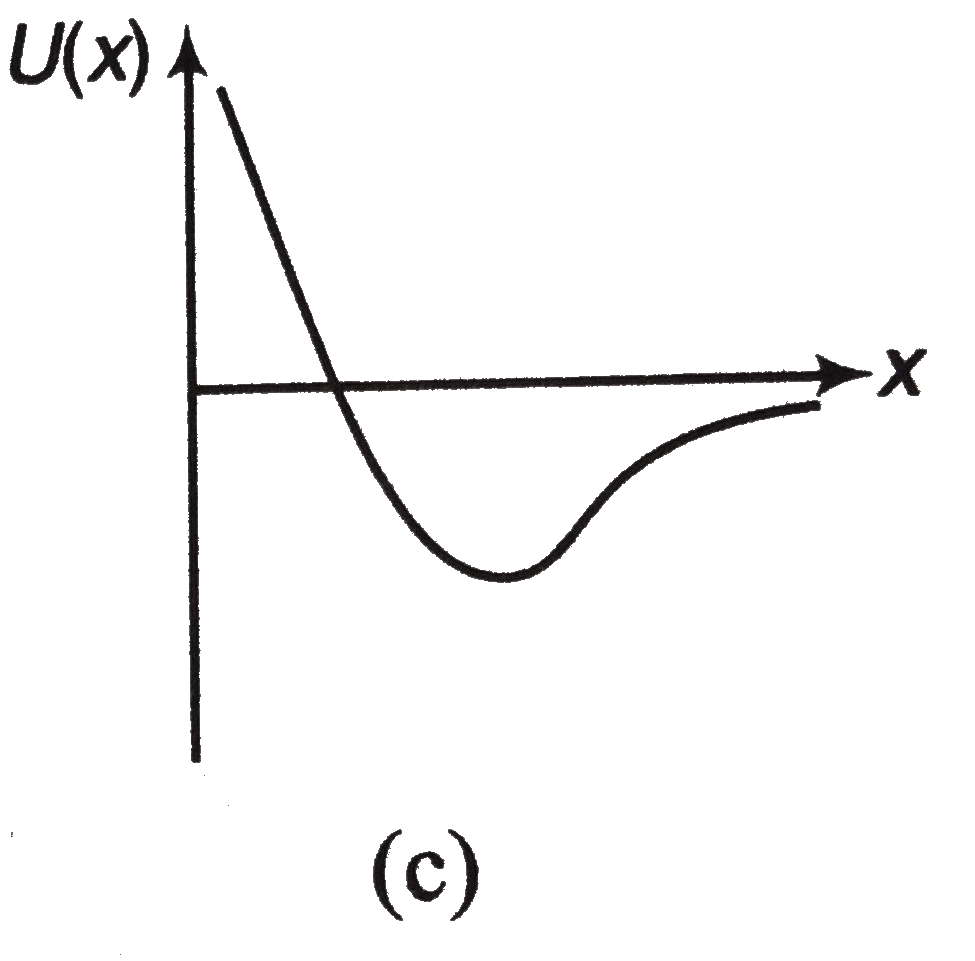 , (d)
, (d) 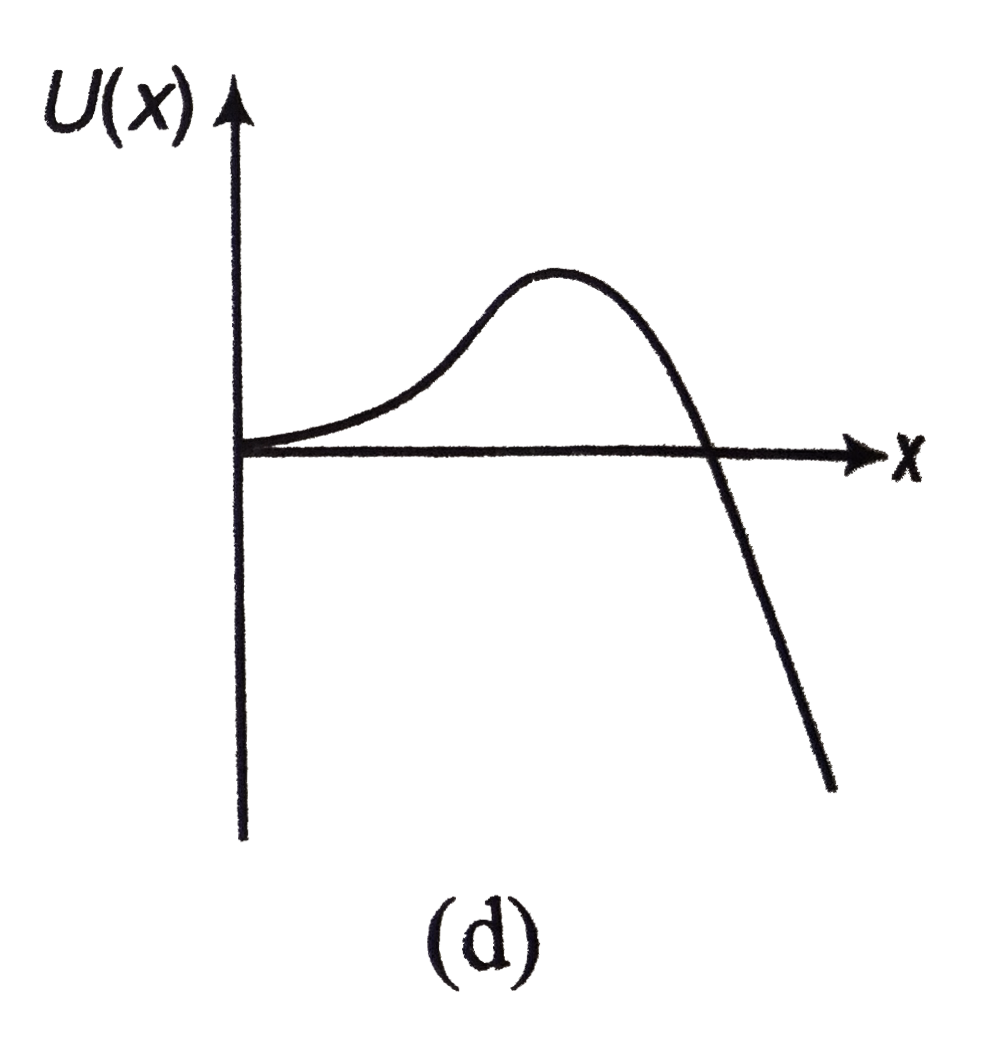 .
.